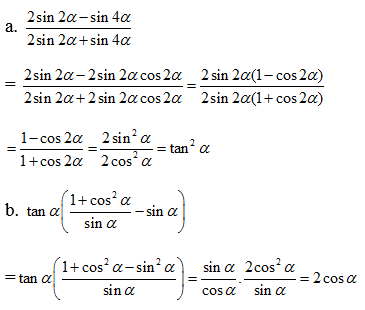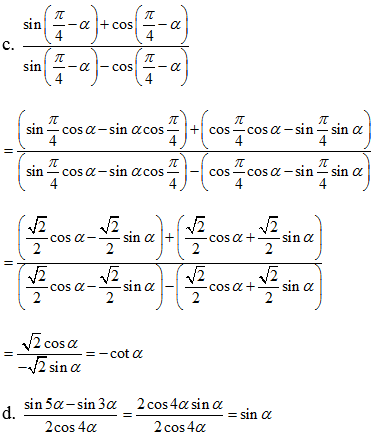Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(sina=\sqrt{1-cos^2a}=\frac{\sqrt{5}}{3}\)
\(cos2a=cos^2a-sin^2a=\frac{4}{9}-\frac{5}{9}=-\frac{1}{9}\)
\(sin4a=2sin2a.cos2a=4sina.cosa.cos2a=4.\frac{\sqrt{5}}{3}.\frac{2}{3}.\left(-\frac{1}{9}\right)=-\frac{8\sqrt{5}}{81}\)

Nhân cả tử và mẫu của phân số chứa tan với \(sina.cosa\)
\(A=\frac{sin^2x-cos^2x}{sin^2x+cos^2x}+cos2x=sin^2x-cos^2x+cos2x=-cos2x+cos2x=0\)
\(B=\frac{1+sin4a-cos4a}{1+sin4a+cos4a}=\frac{1+2sin2a.cos2a-\left(1-2sin^22a\right)}{1+2sin4a.cos4a+2cos^22a-1}\)
\(B=\frac{2sin2a\left(sin2a+cos2a\right)}{2cos2a\left(sin2a+cos2a\right)}=\frac{sin2a}{cos2a}=tan2a\)
\(C=\frac{3-4cos2a+2cos^22a-1}{3+4cos2a+2cos^22a-1}=\frac{2\left(cos^22a-2cos2a-1\right)}{2\left(cos^22a+2cos2a+1\right)}\)
\(C=\frac{\left(cos2a-1\right)^2}{\left(cos2a+1\right)^2}=\frac{\left(1-2sin^2a-1\right)^2}{\left(2cos^2a-1+1\right)^2}=\frac{sin^4a}{cos^4a}=tan^4a\)
\(D=\frac{sin^22a+4sin^4a-\left(2sina.cosa\right)^2}{4-4sin^2a-sin^22a}=\frac{sin^22a+4sin^4a-sin^22a}{4\left(1-sin^2a\right)-\left(2sina.cosa\right)^2}=\frac{4sin^4a}{4cos^2a-4sin^2a.cos^2a}\)
\(=\frac{sin^4a}{cos^2a\left(1-sin^2a\right)}=\frac{sin^4a}{cos^2a.cos^2a}=\frac{sin^4a}{cos^4a}=tan^4a\)

bổ sung đề
với f không giảm
tính f\(\left(\frac{1}{n}\right)\) với n∈\(\left\{1;2;3;....;20\right\}\)