
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Phần bên trên giải thích rồi còn gì
n + n - 1 + n - 2 + n - 3 + .... + 1
Tổng của dãy số hơn kém 1 đơn vị lùi từ n về 1
T = (Số đầu - số cuối) . số số hạng rồi chia 2
tức là \(\dfrac{\left(n-1\right).n}{2}\)

a/ \(y=cos^34x\)
\(y'=3cos^24x.\left(cos4x\right)'=-12.cos^24x.sin4x\)
b/ \(y=sin^23x\)
\(y'=2sin3x.\left(sin3x\right)'=6sin3x.cos3x=3sin6x\)

k ở đây được hiểu là "một số nguyên bất kì", giống hay khác nhau đều được
Ví dụ:
\(sinx=\dfrac{1}{2}\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{6}+k2\pi\\x=\dfrac{5\pi}{6}+k2\pi\end{matrix}\right.\)
Thì "k" trong \(\dfrac{\pi}{6}+k2\pi\) và "k" trong \(\dfrac{5\pi}{6}+k2\pi\) không liên quan gì đến nhau (nó chỉ là 1 kí hiệu, có thể k trên bằng 0, k dưới bằng 100 cũng được, không ảnh hưởng gì, cũng có thể 2 cái bằng nhau cũng được).
Khi người ta ghi 2 nghiệm đều là "k2pi" chủ yếu do... lười biếng (kiểu như mình). Trên thực tế, rất nhiều tài liệu cũ họ ghi các kí tự khác nhau, ví dụ 1 nghiệm là \(\dfrac{\pi}{6}+k2\pi\), 1 nghiệm là \(\dfrac{5\pi}{6}+n2\pi\) để tránh học sinh phát sinh hiểu nhầm đáng tiếc rằng "2 cái k phải giống hệt nhau về giá trị".

ĐKXĐ:
\(\frac{1+x}{1-x}\ge0\Leftrightarrow-1\le x< 1\)
Hay \(D=[-1;1)\)

Bạn sai ở chỗ này:
\(2cos2x=2cos2x.sinx\)
\(\Leftrightarrow sinx=\frac{2cos2x}{2cos2x}\)
Đúng ra phải là: \(\Leftrightarrow2cos2x.sinx-2cos2x=0\)
\(\Leftrightarrow2cos2x\left(sinx-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cos2x=0\\sinx=1\end{matrix}\right.\)

\(\Leftrightarrow2cos^2x-1-\left(2m-3\right)cosx+m-1=0\)
\(\Leftrightarrow2cos^2x-\left(2m-3\right)cosx+m-2=0\)
\(\Leftrightarrow\left(2cosx-1\right)\left(cosx-m+2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cosx=\dfrac{1}{2}\\cosx=m-2\end{matrix}\right.\)
Do \(cosx=\dfrac{1}{2}\Rightarrow x=\dfrac{\pi}{3}+k2\pi\) ko có nghiệm thuộc khoảng đã chi
\(\Rightarrow cosx=m-2\) có nghiệm thuộc \(\left(\dfrac{\pi}{2};\dfrac{3\pi}{2}\right)\)
Ta có \(x\in\left(\dfrac{\pi}{2};\dfrac{3\pi}{2}\right)\Rightarrow cosx\in\left(-1;0\right)\)
\(\Rightarrow-1< m-2< 0\)
\(\Rightarrow1< m< 2\)

\(\Leftrightarrow cosx+sinx+\dfrac{cosx+sinx}{sinx-cosx}=0\)
\(\Leftrightarrow\left(cosx+sinx\right)\left(1+\dfrac{1}{sinx-cosx}\right)=0\)
Chuyển vế rồi đặt nhân tử chung thôi em

Cho hình chóp S.abcd đáy abcd là hình thang (ab//cd) điểm M thuộc SB
Tìm giao tuyến của mặt phẳng (MAD) và mặt phẳng (SBC)

Lời giải:
Bạn sử dụng công thức tính tổ hợp chập thôi
\(15C^k_n=7C^{k+1}_n\Leftrightarrow 15.\frac{n!}{k!(n-k)!}=7.\frac{n!}{(k+1)!(n-k-1)!}\)
\(\Leftrightarrow 15.\frac{n!}{k!(n-k-1)!(n-k)}=7.\frac{n!}{k!(k+1)(n-k-1)!}\)
\(\Leftrightarrow \frac{15}{n-k}=\frac{7}{k+1}\Rightarrow 15(k+1)=7(n-k)\)
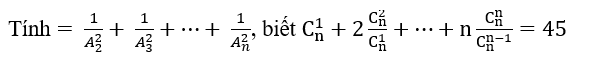
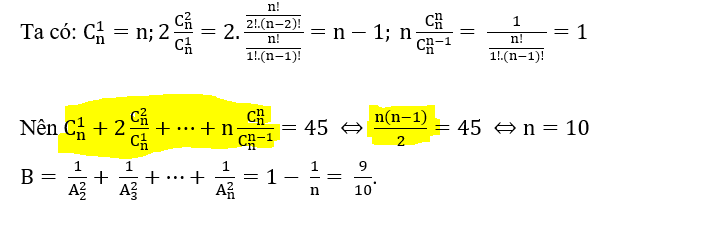
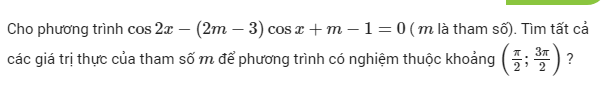

Về bản chất thì đây là một ánh xạ \(u\) có tập xác định là \(ℕ^∗\) còn tập giá trị là \(ℝ\). Lấy ví dụ, xét ánh xạ:
\(u:ℕ^∗\rightarrowℝ\)
\(x\rightarrow\sqrt{x}\)
Khi đó nếu ta lấy \(x\inℕ^∗\) thì sẽ cho ra \(\sqrt{x}\inℝ\).
Ánh xạ \(u:ℕ^∗\rightarrowℝ\) là định nghĩa cơ bản của dãy số \(\left(u_n\right)_{n\ge1}\)