ND
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
24 tháng 4 2017
Hướng dẫn giải:
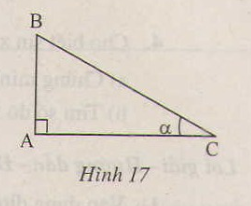
a) tgα=ABAC=AB⋅BCAC⋅BCtgα=ABAC=AB⋅BCAC⋅BC
⇒tgα=ABBC÷ACBC=sinαcosα⇒tgα=ABBC÷ACBC=sinαcosα
tgα⋅cotgα=ABAC⋅ACAB=1tgα⋅cotgα=ABAC⋅ACAB=1
cotgα=1tgα=1sinαcosα=cosαsinαcotgα=1tgα=1sinαcosα=cosαsinα
b) sin2α+cos2α=AB2BC2+AC2BC2=BC2BC2=1sin2α+cos2α=AB2BC2+AC2BC2=BC2BC2=1
Nhận xét: Ba hệ thức tgα=sinαcosαtgα=sinαcosα
cotgα=cosαsinα;sin2α+cos2α=1cotgα=cosαsinα;sin2α+cos2α=1 là những hệ thức cơ bản bạn cần nhớ để giải một số bài tập khá
24 tháng 4 2017
a) tgα=ABAC=AB⋅BCAC⋅BCtgα=ABAC=AB⋅BCAC⋅BC
⇒tgα=ABBC÷ACBC=sinαcosα⇒tgα=ABBC÷ACBC=sinαcosα
tgα⋅cotgα=ABAC⋅ACAB=1tgα⋅cotgα=ABAC⋅ACAB=1
cotgα=1tgα=1sinαcosα=cosαsinαcotgα=1tgα=1sinαcosα=cosαsinα
b) sin2α+cos2α=AB2BC2+AC2BC2=BC2BC2=1sin2α+cos2α=AB2BC2+AC2BC2=BC2BC2=1
Nhận xét: Ba hệ thức tgα=sinαcosαtgα=sinαcosα
cotgα=cosαsinα;sin2α+cos2α=1cotgα=cosαsinα;sin2α+cos2α=1 là những hệ thức cơ bản bạn cần nhớ để giải một số bài tập khác.
NT
1
22 tháng 7 2018
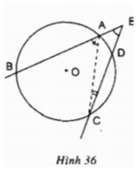
Cho tam giác ABC có trực tâm H , trọng tâm G , O là tâm đường tròn
ngoại tiếp , I là trung điểm BC , AD là đường kính của (O) .
Chứng minh H , G , O thẳng hàng ?
Giải :
Ta có : góc DCA = góc DBA = 90 độ ( góc nội tiếp chắn 1/2 (O))
Xét tứ giác BHCD ta có :
BH // DC ( vì cùng vuông góc với AC )
CH // DB ( vì cùng vuông góc với AB )
Do đó tứ giác BHCD là hình bình hành .
===> H , I , D thẳng hàng và IH = ID (t/c đường chéo hbhành)
Ta lại có : OI = 1/2 AH ( đ.trung bình tam giác DAH ) (1)
GI = 1/2 GA (t/chất trọng tâm của ABC ) (2)
góc HAG = góc GIO ( so le trong vì AH // OI ) (3)
Do đó tam giác GAH đồng dạng tam giác GIO ( c.g.c)
===> góc HGA = góc IGO (góc tương ứng của 2 t.giác đ.dạng )
Vì góc HGA và góc IGO là 2 góc ở vị trí đối đỉnh bằng nhau nên ta suy ra H , G , O thẳng hàng .
Vậy trong 1 tam giác trực tâm , trọng tâm , tâm đường tròn ngoại tiếp cùng nằm trên 1 đường thẳng đó là đường thẳng Euler !
hok tốt
10 tháng 4 2018
a) Định lí đảo ”Nếu n là số nguyên dương sao cho 5n + 6 là số lẻ thì n là số lẻ". Phát biểu gộp cả định lí thuận và định lí đảo là “Với mọi số nguyên dương n, 5n + 6 là số lẻ khi và chỉ khi n là số lẻ”.
b) Định lí đảo “Nếu n là số nguyên dương sao cho 7n + 4 là số chẵn thì n là số chẵn”. Phát biểu gộp cả hai định lí thuận và đảo là: “với mọi số nguyên dương n, 7n + 4 là số chẵn khi và chỉ khi n là số chẵn”.
11 tháng 4 2018
a) Định lí đảo ”Nếu n là số nguyên dương sao cho 5n + 6 là số lẻ thì n là số lẻ". Phát biểu gộp cả định lí thuận và định lí đảo là “Với mọi số nguyên dương n, 5n + 6 là số lẻ khi và chỉ khi n là số lẻ”
b) Định lí đảo “Nếu n là số nguyên dương sao cho 7n + 4 là số chẵn thì n là số chẵn”. Phát biểu gộp cả hai định lí thuận và đảo là: “với mọi số nguyên dương n, 7n + 4 là số chẵn khi và chỉ khi n là số chẵn”.
PT
0
Trong một tam giác vuông, bình phương của cạnh huyền bằng tổng các bình phương của hai cạnh góc vuông.
Định lý pytago là mối liên hệ căn bản trong hình học Euclid giữa ba cạnh của một tam giác vuông. Định lý phát biểu rằng bình phương cạnh huyền (cạnh đối diện với góc vuông) bằng tổng bình phương của hai cạnh còn lại.