Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B C H
a) XÉT tam giác HAC (\(\widehat{H}\)=\(90^O\)) CÓ
AH là đường vuông góc của hình xiên AC
\(\Rightarrow AC>AH\) (quan hệ giữa đường vuông góc và hình xiên trong tam giác) (đpcm)
b) Xét tam giác HAB (\(\widehat{H}=90^o\)) có
AH là đường vuông góc của đường xiên AB
\(\Rightarrow AB>AH\)(quan hệ giữa đường vuông góc và hình xiên) (đpcm)

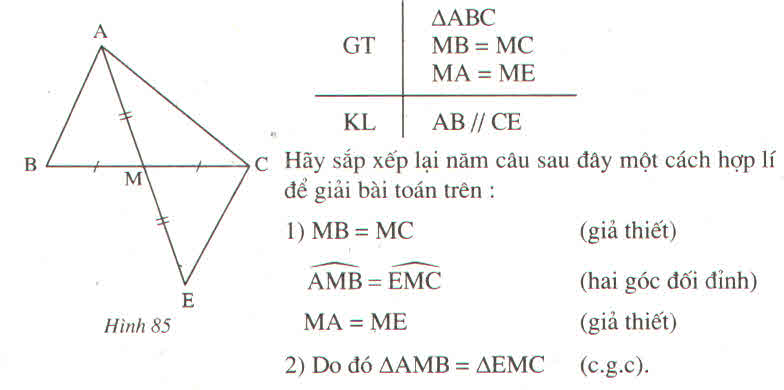
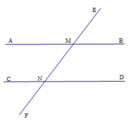
Ta có: AME ^ + EMB ^ = 180 ∘ (hai góc kề bù)
Mà AME ^ = 3 EMB ^
⇒ 3 EMB ^ + EMB ^ = 180 ∘
⇒ 4 EMB ^ = 180 ∘
⇒ EMB ^ = 180 ∘ : 4
⇒ EMB ^ = 45 ∘ (1)
Ta có: AME ^ + EMB ^ + MND ^ = 225 ∘
⇒ 180 ∘ + MND ^ = 225 ∘
⇒ MND ^ = 225 ∘ − 180 ∘
⇒ MND ^ = 45 ∘ (2)
Từ (1) và (2) suy ra EMB ^ = MND ^ mà hai góc này ở vị trí đồng vị
AB // CD
Hai đường thẳng AB và AC trùng nhau.
Hai đường thẳng a và b song song. Ký hiệu: a // b
Hai đường thẳng m và n cắt nhau.
Hai đường thẳng d và d’ vuông góc với nhau . Ký hiệu: d ⊥ d’