Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi A,B lần lượt là giao của (d) với trục Ox và Oy
Tọa độ A là:
y=0 và (2m+1)x-1=0
=>x=1/(2m+1) và y=0
=>OA=1/|2m+1|
Tọa độ B là:
x=0 và y=-1
=>OB=1
Theo đề, ta có: S OAB=1/2
=>1/2*OA*OB=1/2
=>1/|2m+1|=1
=>|2m+1|=1
=>2m+1=1 hoặc 2m+1=-1
=>m=-1 hoặc m=0

\(\left(m+1\right)x+\left(m-2\right)y=3\)\(\left(m\ne-1;m\ne2\right)\)
\(y=0\Leftrightarrow x=\dfrac{3}{m+1}\Rightarrow A\left(\dfrac{3}{m+1};0\right)\Rightarrow OA=\left|\dfrac{3}{m+1}\right|\)
\(x=0\Leftrightarrow y=\dfrac{3}{m-2}\Leftrightarrow B\left(0;\dfrac{3}{m-2}\right)\Rightarrow OB=\left|\dfrac{3}{m-2}\right|\)
\(S_{_{ }^{ }\Delta ABO}=\dfrac{9}{2}=\dfrac{1}{2}OA.OB=\dfrac{1}{2}.\dfrac{9}{\left|m+1\right|.\left|m-2\right|}\Leftrightarrow\dfrac{1}{\left|m+1\right|.\left|m-2\right|}=9\Leftrightarrow\left|m+1\right|.\left|m-2\right|=9\Leftrightarrow\left(m+1\right)^2.\left(m-2\right)^2-81=0\Leftrightarrow\left(m^2-m-11\right)\left(m^2-m+7\right)=0\Leftrightarrow\left[{}\begin{matrix}m^2-m-11=0\Leftrightarrow m=\dfrac{1\pm3\sqrt{5}}{2}\left(tm\right)\\m^2-m+7=0\left(vô-nghiệm\right)\end{matrix}\right.\)
\(\Rightarrow m=\dfrac{1\pm3\sqrt{5}}{2}\)
Cho x = 0 => \(y=\dfrac{3}{m-2}\)
vậy d cắt Oy tại A(0;3/m-2) => Oy = \(\left|\dfrac{3}{m-2}\right|\)
Cho y = 0 => \(x=\dfrac{3}{m+1}\)
vậy d cắt Ox tại B(3/m+1;0) => Ox = \(\left|\dfrac{3}{m+1}\right|\)
Ta có : \(S_{OAB}=\dfrac{1}{2}.OB.OA=\dfrac{1}{2}.\dfrac{9}{\left|\left(m+1\right)\left(m-2\right)\right|}=\dfrac{9}{2}\)
\(\Leftrightarrow\left|\left(m+1\right)\left(m-2\right)\right|=1\Leftrightarrow\left[{}\begin{matrix}m^2-m-3=0\\m^2-m-1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}m=\dfrac{1+\sqrt{13}}{2};m=\dfrac{1-\sqrt{13}}{2}\\m=\dfrac{1+\sqrt{5}}{2};m=\dfrac{1-\sqrt{5}}{2}\end{matrix}\right.\)

d ∩ O y = B ⇒ x B = 0 ⇒ y B = − 1 ⇒ B 0 ; − 1 ⇒ O B = − 1 = 1 d ∩ O x = A ⇒ y A = 0 2 m + 1 x – 1 = 0 ⇔ x A = 1 2 m + 1 m ≠ − 1 2
⇒ A 1 2 m + 1 ; 0 ⇒ O A = 1 2 m + 1
S Δ A O B = 1 2 O A . O B = 1 2 .1. 1 2 m + 1 = 1 2 ⇔ | 2 m + 1 | = 1 ⇔ m = 0 m = − 1
Đáp án cần chọn là: D

c) y = (m – 3)x + 2 (m ≠ 3)
Gọi A, B lần lượt là giao điểm của (d) và trục Ox, Oy và tam giác tạo thành là tam giác AOB vuông tại O
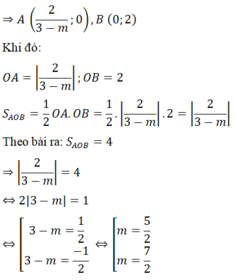

+ x =0 => y =-3 A(0;-3)
+ m khác 2 => y =0 => x =3/(m-2) B(3/(m-2) ;0)
S =OA.OB/2 =2 => OA.OB=4
=> 3.3/ (/m-2/) =4 => /m-2/ =9/4 => m =2+9/4=17/4 (TM)
hoặc m=2 -9/4 = -1/4 (TM)
Gọi A,B lần lượt là giao điểm của (d) với trục Ox và Oy
Tọa độ A là:
\(\left\{{}\begin{matrix}y=0\\\left(2m+1\right)x-2=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=0\\x\left(2m+1\right)=2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=0\\x=\dfrac{2}{2m+1}\end{matrix}\right.\)
=>\(A\left(\dfrac{2}{2m+1};0\right)\)
\(OA=\sqrt{\left(\dfrac{2}{2m+1}-0\right)^2+\left(0-0\right)^2}=\sqrt{\left(\dfrac{2}{2m+1}\right)^2}=\dfrac{2}{\left|2m+1\right|}\)
Tọa độ B là:
\(\left\{{}\begin{matrix}x=0\\y=\left(2m+1\right)x-2=0\cdot\left(2m+1\right)-2=-2\end{matrix}\right.\)
=>B(0;-2)
\(OB=\sqrt{\left(0-0\right)^2+\left(-2-0\right)^2}=\sqrt{0+4}=2\)
Vì Ox\(\perp\)Oy
nên OA\(\perp\)OB
=>ΔOAB vuông tại O
=>\(S_{OAB}=\dfrac{1}{2}\cdot OA\cdot OB=\dfrac{1}{2}\cdot2\cdot\dfrac{2}{\left|2m+1\right|}=\dfrac{2}{\left|2m+1\right|}\)
Để \(S_{OAB}=1\) thì \(\dfrac{2}{\left|2m+1\right|}=1\)
=>|2m+1|=2
=>\(\left[{}\begin{matrix}2m+1=2\\2m+1=-2\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}2m=1\\2m=-3\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}m=\dfrac{1}{2}\\m=-\dfrac{3}{2}\end{matrix}\right.\)