Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a. phương trình tham số d có dạng : \(\left\{{}\begin{matrix}x=2+3t\\y=1+4t\end{matrix}\right.\)
b. phương trình tham số d có dạng: \(\left\{{}\begin{matrix}x=-2+5t\\y=3+t\end{matrix}\right.\)
a) \(\left\{{}\begin{matrix}x=-5+4t\\y=-2-3t\end{matrix}\right.\)
b) \(\left\{{}\begin{matrix}x=\sqrt{3}+2t\\y=1+3t\end{matrix}\right.\)
Bài 2:
Phương trình (d) cần tìm là -3(x-1)+5(y-3)=0
=>-3x+3+5y-15=0
=>-3x+5y-12=0
=>3x-5y+12=0
Bài 3:
vecto chỉ phương là \(\overrightarrow{v}=\left(-3;5\right)\)
=>VTPT là (5;3)
Phương trình đường thẳng là:
5(x-5)+3(y-3)=0
=>5x-25+3y-9=0
=>5x+3y-34=0
Chọn B.
Phương trình tổng quát là:
2.(x - 3) + 1.(y - 2) = 0
⇒ 2x - 6 + y - 2 = 0
⇔ 2x + y - 8 = 0
a. Md1= (2;1)
Md2 = (-1;3)
b. Gọi d là đường thẳng đi qua M
- Viết PTTS của d ⊥ d1:
Ta có:
M(2;1)
Do d1⊥ d nên VTCP ud1 = (-3;-1) --> VTPT nd = (-1;3)
--> VTCP ud = (3;1)
Vậy PTTS của d:
\(\left\{{}\begin{matrix}x=2+3t\\y=1+t\end{matrix}\right.\)
- Viết PTTQ của d ⊥ d1:
Ta có:
M(2;1)
Do d1 ⊥ d nên VTCP ud1 = (-3;-1) --> VTPT nd = (-1;3)
Vậy PTTQ của d:
-1(x - 2) + 3(y - 1) = 0
<=> -x + 2 + 3y - 3 = 0
<=> -x + 3y - 1 = 0
- Viết PTTS của d ⊥ d2:
Ta có:
M(-1;3)
Do d ⊥ d2 nên VTCP ud2 = (-2;-1) --> VTPT ud = (-1;2)
--> VTCP ud = (2;1)
Vậy PTTS của d:
\(\left\{{}\begin{matrix}x=-1+2t\\y=3+t\end{matrix}\right.\)
Viết PTTQ của d ⊥ d2:
M(-1;3)
Do d ⊥ d2 nên VTCP ud2 = (-2;-1) --> VTPT ud = (-1;2)
Vậy PTTQ của d:
-1(x + 1) + 2(y - 3) = 0
<=> -x - 1 + 2y - 6 = 0
<=> -x + 2y - 7 = 0
Bài 1:
\(2c=8\Rightarrow c=4\)
Gọi phương trình (E) có dạng \(\frac{x^2}{a^2}+\frac{y^2}{a^2-16}=1\)
Do A thuộc (E) nên \(\frac{0}{a^2}+\frac{9}{a^2-16}=1\Rightarrow a^2=25\)
Phương trình (E): \(\frac{x^2}{25}+\frac{y^2}{9}=1\)
Bài 2:
\(2a=10\Rightarrow a=5\)
\(e=\frac{c}{a}\Rightarrow c=e.a=\frac{3}{5}.5=3\)
Phương trình elip:
\(\frac{x^2}{25}+\frac{y^2}{16}=1\)
Câu 3:
\(x-2y+3=0\Rightarrow x=2y-3\)
Thay vào pt đường tròn ta được:
\(\left(2y-3\right)^2+y^2-2\left(2y-3\right)-4y=0\)
\(\Leftrightarrow5y^2-20y+15=0\)
\(\Rightarrow\left[{}\begin{matrix}y=1\Rightarrow x=-1\\y=3\Rightarrow x=3\end{matrix}\right.\)
Tọa độ 2 giao điểm: \(A\left(-1;1\right)\) và \(B\left(3;3\right)\)
Câu 4:
Gọi d' là đường thẳng song song với d \(\Rightarrow\) pt d' có dạng \(x-y+c=0\)
Do d' tiếp xúc với (C) nên \(d\left(I;d'\right)=R\)
\(\Rightarrow\frac{\left|0.1-0.1+c\right|}{\sqrt{1^2+1^2}}=\sqrt{2}\Rightarrow\left|c\right|=2\Rightarrow c=\pm2\)
Có 2 pt đường thẳng thỏa mãn: \(\left[{}\begin{matrix}x-y+2=0\\x-y-2=0\end{matrix}\right.\)
a) Đường thẳng \(d\) đi qua điểm \(A( - 1;5)\) và có vectơ chỉ phương \(\overrightarrow u = \left( {2;1} \right)\), nên có phương trình tham số là:
\(\left\{ \begin{array}{l}x = - 1 + 2t\\y = 5 + t\end{array} \right.\)
Đường thẳng \(d\) có vectơ chỉ phương \(\overrightarrow u = \left( {2;1} \right)\),nên có vectơ pháp tuyền là \(\overrightarrow n = \left( {1; - 2} \right)\) và đi qua \(A( - 1;5)\)
Ta có phương trình tổng quát là
\((x + 1) - 2(y - 5) = 0 \Leftrightarrow x - 2y + 11 = 0\)
b) Đường thẳng \(d\) có vectơ pháp tuyến \(\overrightarrow n = \left( {3; - 2} \right)\) nên có vectơ chỉ phương \(\overrightarrow u = \left( {2;3} \right)\), và đi qua điểm \(B(4; - 2)\) nên ta có phương trình tham số của \(d\) là :
\(\left\{ \begin{array}{l}x = 4 + 2t\\y = - 2 + 3t\end{array} \right.\)
Đường thẳng \(d\) đi qua điểm \(B(4; - 2)\) và có vectơ pháp tuyến \(\overrightarrow n = \left( {3; - 2} \right)\)
Phương trình tổng quát của đường thẳng d là:
\(3(x - 4) - 2(y + 2) = 0 \Leftrightarrow 3x - 2y - 16 = 0\)
c) Đường thẳng \(d\) có dạng \(y = ax + b\)
d đi qua \(P(1;1)\) và có hệ số góc \(k = - 2\) nên ta có:
\(1 = - 2.1 + b \Rightarrow b = 3\)
Suy ra đồ thị đường thẳng d có dạng \(y = - 2x + 3\)
Vậy đường thẳng d có phương trình tổng quát là \(y + 2x - 3 = 0\)
Suy ra đường thẳng d có vectơ pháp tuyến \(\overrightarrow n = \left( {2;1} \right)\), nên có vectơ chỉ phương là \(\overrightarrow u = \left( {1; - 2} \right)\) và đi qua điểm \(P(1;1)\) nên ta có phương trình tham số của d là :
\(\left\{ \begin{array}{l}x = 1 + t\\y = 1 - 2t\end{array} \right.\)
d) Đường thẳng \(d\) đi qua hai điểm \(Q(3;0)\)và \(R(0;2)\) nên có vectơ chỉ phương \(\overrightarrow u = \overrightarrow {QR} = ( - 3;2)\) và có vectơ pháp tuyến \(\overrightarrow n = (2;3)\)
Phương trình tham số của \(\Delta \) là: \(\left\{ \begin{array}{l}x = 3 - 3t\\y = 2t\end{array} \right.\)
Phương trình tổng quát của \(\Delta \) là: \(2(x - 3) + 3(x - 0) = \Leftrightarrow 2x + 3y - 6 = 0\)
Chọn C.
Phương trình tham số của đường thẳng đi qua M(2;1) nhận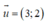
làm VTCP là: