Dựng tam giác ABC cân tại A, biết BC = 3cm, đường cao BH = 2,5 cm

K

Khách

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Mua vip

SG

Sách Giáo Khoa

28 tháng 4 2017

Dựng tam giác ABC cân tại A, biết BC = 3cm, đường cao BH = 2,5 cm

#Hỏi cộng đồng OLM #Toán lớp 8

1

NT

Nguyen Thuy Hoa

29 tháng 6 2017

Dựng hình bằng thước và compa. Dựng hình thang

Các câu hỏi dưới đây có thể giống với câu hỏi trên

PT

Pham Trong Bach

13 tháng 7 2017

Dựng ΔABC cân tại A, biết BC = 3cm, đường cao BH = 2,5cm.

#Hỏi cộng đồng OLM #Toán lớp 8

1

CM

Cao Minh Tâm

13 tháng 7 2017

Giải sách bài tập Toán 8 | Giải bài tập Sách bài tập Toán 8

Cách dựng:

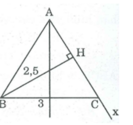
- Dựng BH : 2,5cm

- Dựng ∠ (xHB) = 90 0

- Dựng cung tròn tâm B bán kính 3cm cắt Hx tại C.

- Dựng BC

- Dựng đường trung trực BC cắt CH tại A

- Dựng AB, ta có ∆ ABC cẩn dựng

Chứng minh:

Ta có AC = AB (tính chất đường trung trực)

Nên ∆ ABC cân tại A, BH ⊥ AC

Ta lại có BC = 3cm, BH = 2,5cm

Vậy ∆ ABC dựng được thỏa mãn điều kiện bài toán.

C

Cilina

25 tháng 4 2023

Cho tam giác ABC vuông tại A; đường cao AH ( H thuộc BC ) và phân giác CM ( M thuộc AB ). N là giao điểm AH và CM. Biết BH = 3cm; HC = 27cm. Chứng minh AH² = BH x HC

#Hỏi cộng đồng OLM #Toán lớp 8

1

NL

Nguyễn Lê Phước Thịnh

25 tháng 4 2023

loading...

⊰⊹🅼🅸🅸🅽🅷☠☆

24 tháng 4 2023

cho tam giác ABC cân tại A vẽ đường cao BH CK

a/ cm tam giác BKC đồng dạng tam giác CHB

b/ cm KH//BC

#Hỏi cộng đồng OLM #Toán lớp 8

1

NL

Nguyễn Lê Phước Thịnh

24 tháng 4 2023

a: Xét ΔKBC vuông tại K và ΔHCB vuông tại H co

BC chung

góc KBC=góc HCB

=>ΔKBC đồng dạng với ΔHCB và ΔKCB=ΔHBC

b: AK+KB=AB

AH+HC=AC

mà HC=KB; AB=AC

nên AK=AH

mà AB=AC

nên KH//BC

ND

Nguyễn Đăng Trường

2 tháng 3 2021 - olm

Cho tam giác ABC vuông tại A; đường cao AH ( H thuộc BC ) và phân giác CM ( M thuộc AB ). N là giao điểm AH và CM. Biết BH = 3cm; HC = 27cm. Chứng minh AH² = BH x HC.

#Hỏi cộng đồng OLM #Toán lớp 8

0

SG

Sách Giáo Khoa

28 tháng 4 2017

Dựng hình thang cân ABCD (AB // CD) biết BC = 3cm, AB = 2cm, đường cao bằng 2,5 cm

#Hỏi cộng đồng OLM #Toán lớp 8

1

NT

Nguyen Thuy Hoa

29 tháng 6 2017

Dựng hình bằng thước và compa. Dựng hình thang

A

abcxyz300

18 tháng 8 2021

1.cho tam giác ABC vông tại A, đường cao AH. Biết AB=3cm, BC=5cm. Tính AC, AH, BH, CH 2. Cho tam giác ABC vông tại A, đường cao AH. Biết HB=3,6cm, HC=6,4cm. Tính BC,AB,AC,AH

#Hỏi cộng đồng OLM #Toán lớp 8

2

NL

Nguyễn Lê Phước Thịnh

18 tháng 8 2021

Bài 1:

Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:

\(AB^2+AC^2=BC^2\)

\(\Leftrightarrow AC^2=5^2-3^2=16\)

hay AC=4cm

Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:

\(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}BH=\dfrac{3^2}{5}=1.8\left(cm\right)\\CH=\dfrac{4^2}{5}=3.2\left(cm\right)\end{matrix}\right.\)

Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:

\(AH\cdot BC=AB\cdot AC\)

\(\Leftrightarrow AH\cdot5=3\cdot4=12\)

hay AH=2,4cm

NL

Nguyễn Lê Phước Thịnh

18 tháng 8 2021

Bài 2:

Ta có: BC=HB+HC

nên BC=3,6+6,4

hay BC=10cm

Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:

\(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AB^2=3.6\cdot10=36\\AC^2=6.4\cdot10=64\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AB=6\left(cm\right)\\AC=8\left(cm\right)\end{matrix}\right.\)

Áp dụng định lí Pytago vào ΔABH vuông tại H, ta được:

\(AB^2=AH^2+HB^2\)

\(\Leftrightarrow AH^2=6^2-3.6^2=23.04\)

hay AH=4,8cm

NV

Nguyễn Võ Nhiệt My

16 tháng 11 2016

cho tam giác ABC cân tại B, kẻ đường cao BH. Gọi I là trung điểm của BC, d là điểm đối xứng của H qua I.

a/ Tính diện tích tam giác ABC và độ dài HI. Biết BH= 4 cm, AC= 6 cm

b/ C/m tứ giác BHCD là HCN

c/ Tam giac ABC cân tại B có thêm điều kiện gì thì BHCD là hình vuông

#Hỏi cộng đồng OLM #Toán lớp 8

1

PA

Phương An

16 tháng 11 2016

S_ABC = \(\frac{4\times6}{2}\) = 12 (cm²)

BH là đường cao của tam giác BAC cân tại B.

=> BH là đường trung tuyến của tam giác ABC.

=> H là trung điểm của AC.

=> AH = HC = AC/2 = 6/2 = 3 (cm)

Tam giác HBC vuông tại H có:

BC² = HB² + HC²(định lý Pytago)

= 4² + 3²

= 16 + 9

= 25

BC = \(\sqrt{25}\) = 5 (cm)

Tam giác HBC vuông tại H có HI là đường trung tuyến (I là trung điểm của BC)

=> HI = BC/2 = 5/2 = 2,5 (cm)

I là trung điểm của BC (gt)

I là trung điểm của HD (H đối xứng D qua I)

=> BHCD là hình bình hành.

mà BHC = 90⁰

=> BHCD là hình chữ nhật.

=> BHCD là hình vuông

<=> BH = HC

<=> Tam giác BAC có đường trung tuyến BH bằng 1 nửa cạnh AC.

<=> Tam giác ABC vuông tại B.

mà tam giác BAC cân tại B.

=> Tam giác BAC vuông cân tại B.

Vậy BHCD là hình vuông khi tam giác BAC vuông cân tại B.

H

hjxbwbskewndkndk

29 tháng 4 2022

Cho tam giác ABC vuông tại A có AB=3cm, BC=5cm, vẽ đường cao AH của tam giác ABC.

a) CM: tam giác ABC~ tam giác HBA

b) CM: AB^2=BH.BC, tính BH

c) Dựng đường p/g BD của tam giác ABC cắt AH ở E. Tính EH/EA. Tính EH

d) Tính diện tích tứ giác HEDC

#Hỏi cộng đồng OLM #Toán lớp 8

1

NL

Nguyễn Lê Phước Thịnh

30 tháng 4 2022

a: XétΔABC vuông tại A và ΔHBA vuông tại H có

góc B chung

Do đó:ΔABC\(\sim\)ΔHBA

b: Ta có: ΔABC\(\sim\)ΔHBA

nên BA/BH=BC/BA

hay \(BA^2=BH\cdot BC\)

\(BH=\dfrac{BA^2}{BC}=\dfrac{3^2}{5}=1.8\left(cm\right)\)

TT

Tuấn Tú

2 tháng 5 2023

Cho tam giác ABC cân tại A.Vẽ các đường cao BH, CK.
a) CM BK=CH
b) CM HK//BC
c) Cho AB=6cm, BC=4cm. Tính HK

#Hỏi cộng đồng OLM #Toán lớp 8

1

NL

Nguyễn Lê Phước Thịnh

12 tháng 5 2023

a: Xét ΔKBC vuông tại K và ΔHCB vuông tại H có

BC chung

góc KBC=goc HCB

=>ΔKBC=ΔHCB

=>BK=HC

=>AK=AH

b: Xét ΔABC có AK/AB=AH/AC

nên KH//BC