Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tham khảo:
- Cách xác định bước sóng do hai nguồn phát ra:
+ Đo khoảng cách giữa hai nguồn.
+ Đếm số khoảng cách giữa đỉnh hai gợn lồi liên tiếp hoặc số khoảng cách giữa đỉnh hai gợn lõm liên tiếp do hai nguồn tạo ra.
+ Dựa vào khái niệm bước sóng là khoảng cách gần nhau nhất giữa hai gợn lồi hoặc hai gợn lõm.
- Áp dụng:
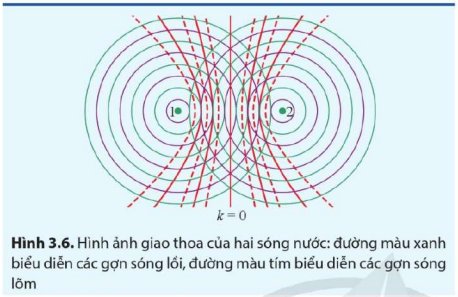
+ Giả sử đối với hình 3.6 ở trên ta đo được khoảng cách giữa hai nguồn S1S2 = a
+ Khoảng giữa hai nguồn có 4 gợn lồi (không tính 2 nguồn) bằng 3.
Khi đó hoàn toàn tính được bước sóng \(\lambda=\dfrac{a}{3}\)

Tham khảo:
Hai nguồn dao động cùng pha nên những điểm thuộc đường trung trực của đoạn nối hai nguồn là những điểm có biên độ cực đại.
Gọi điểm M là điểm cách hai nguồn các khoảng lần lượt là 20 cm và 12 cm, sóng có biên độ cực đại: \(d_2-d_1=20-12=8k\lambda\)
Do giữa điểm M và đường trung trực của hai nguồn có 4 dãy gồm những điểm dao động với biên độ cực đại nên M thuộc dãy cực đại bậc 5.
\(\Rightarrow k=5\Rightarrow\lambda=\dfrac{8}{5}1,6\left(cm\right)\Rightarrow f=\dfrac{v}{\lambda}=\dfrac{40}{1,6}=25Hz\)

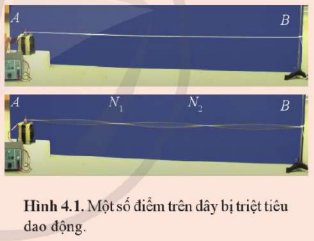
Tần số sóng trên dây càng lớn, số bụng sóng càng nhiều. Số bụng sóng tỉ lệ với tần số sóng.

a. Dựa vào đồ thị ta có:
Chu kì \(T = 2 s\), suy ra tần số góc \(\omega = \frac{2 \pi}{T} = \frac{2 \pi}{2} = \pi\) rad/s
Vận tốc cực đại của dao động: \(\text{v}_{m a x} = \omega A\)
\(\Rightarrow A = \frac{\text{v}_{m a x}}{\omega} = \frac{4}{\pi}\) cm
Thời điểm \(t = 0\), vật có \(\text{v} = \text{v}_{m a x}\), suy ra vật ở VTCB và \(\text{v} > 0\)
Khi đó: \(x = 0 \Rightarrow cos \varphi = 0 \Rightarrow \varphi = - \frac{\pi}{2}\)
Phương trình của vận tốc có dạng: \(\text{v} = \omega A cos \left(\right. \omega t + \varphi + \frac{\pi}{2} \left.\right)\)
\(\Rightarrow \text{v} = 4 cos \left(\right. \pi t - \frac{\pi}{2} + \frac{\pi}{2} \left.\right) = 4 cos \left(\right. \pi t \left.\right)\) (cm/s)
b. Phương trình dao động điều hòa có dạng: \(x = A cos \left(\right. \omega t + \varphi \left.\right)\)
\(\Rightarrow x = \frac{4}{\pi} cos \left(\right. \pi t - \frac{\pi}{2} \left.\right)\) (cm)
Phương trình của gia tốc có dạng: \(a = \omega^{2} A cos \left(\right. \omega t + \varphi + \pi \left.\right)\)
\(\Rightarrow a = \pi^{2} . \frac{4}{\pi} cos \left(\right. \pi t - \frac{\pi}{2} + \pi \left.\right) = 4 \pi cos \left(\right. \pi t + \frac{\pi}{2} \left.\right)\) (cm/s2)






Nối các điểm giao nhau giữa các gợn lồi hoặc của các gợn lõm của hai nguồn sóng với mỗi nguồn, đo khoảng cách \(x_1,x_2\). Tính \(\dfrac{x_1-x_2}{\lambda}\) với \(\lambda\) được xác định trong câu hỏi trước. Nếu thương số nhận được là một số nguyên thì kết quả đúng với công thức.