Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có:
\(W_t=\dfrac{1}{2}m\omega^2A^2cos^2\left(\omega t+\varphi_0\right)\\ W_d=\dfrac{1}{2}mv^2=\dfrac{1}{2}m\omega^2A^2sin^2\left(\omega t+\varphi_0\right)\\ \Rightarrow W=W_t+W_d=\dfrac{1}{2}m\omega^2A^2\left[cos^2\left(\omega t+\varphi_0\right)+sin^2\left(\omega t+\varphi_0\right)\right]\\ \Rightarrow W=\dfrac{1}{2}m\omega^2A^2\)

Công thức (3.5): \(W_d=\dfrac{1}{2}mw^2A^2sin^2\left(wt+\varphi_0\right)\)
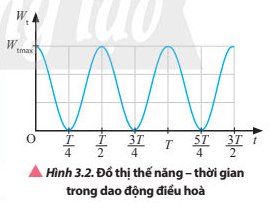
Đồ thị động năng – thời gian cũng có dạng hình sin.
Từ đồ thị ta thấy:
+ Tại thời điểm ban đầu, động năng bằng 0
+ Tại thời điểm \(\dfrac{T}{4}\), động năng cực đại
+ Tại thời điểm \(\dfrac{T}{2}\), động năng bằng 0
+ Tại thời điểm \(\dfrac{3T}{4}\), động năng cực đại
+ Tại thời điểm T, động năng bằng 0.

a. Dựa vào đồ thị ta có:
Chu kì \(T = 2 s\), suy ra tần số góc \(\omega = \frac{2 \pi}{T} = \frac{2 \pi}{2} = \pi\) rad/s
Vận tốc cực đại của dao động: \(\text{v}_{m a x} = \omega A\)
\(\Rightarrow A = \frac{\text{v}_{m a x}}{\omega} = \frac{4}{\pi}\) cm
Thời điểm \(t = 0\), vật có \(\text{v} = \text{v}_{m a x}\), suy ra vật ở VTCB và \(\text{v} > 0\)
Khi đó: \(x = 0 \Rightarrow cos \varphi = 0 \Rightarrow \varphi = - \frac{\pi}{2}\)
Phương trình của vận tốc có dạng: \(\text{v} = \omega A cos \left(\right. \omega t + \varphi + \frac{\pi}{2} \left.\right)\)
\(\Rightarrow \text{v} = 4 cos \left(\right. \pi t - \frac{\pi}{2} + \frac{\pi}{2} \left.\right) = 4 cos \left(\right. \pi t \left.\right)\) (cm/s)
b. Phương trình dao động điều hòa có dạng: \(x = A cos \left(\right. \omega t + \varphi \left.\right)\)
\(\Rightarrow x = \frac{4}{\pi} cos \left(\right. \pi t - \frac{\pi}{2} \left.\right)\) (cm)
Phương trình của gia tốc có dạng: \(a = \omega^{2} A cos \left(\right. \omega t + \varphi + \pi \left.\right)\)
\(\Rightarrow a = \pi^{2} . \frac{4}{\pi} cos \left(\right. \pi t - \frac{\pi}{2} + \pi \left.\right) = 4 \pi cos \left(\right. \pi t + \frac{\pi}{2} \left.\right)\) (cm/s2)

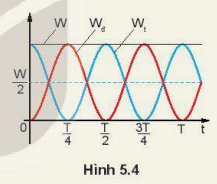
a) Từ 0 đến \(\frac{T}{4}\): Wđ tăng từ 0 đến giá trị lớn nhất tại \(\frac{T}{4}\), Wt giảm từ giá trị lớn nhất về 0 tại \(\frac{T}{4}\).
Từ \(\frac{T}{4}\)đến \(\frac{T}{2}\): Wđ giảm từ giá trị lớn nhất về 0 tại \(\frac{T}{2}\), Wt tăng từ 0 đến giá trị lớn nhất tại \(\frac{T}{2}\).
Từ \(\frac{T}{2}\)đến \(\frac{{3T}}{4}\): Wđ tăng từ 0 đạt giá trị lớn nhất tại \(\frac{{3T}}{4}\),Wt giảm từ giá trị lớn nhất về 0 tại \(\frac{{3T}}{4}\).
Từ \(\frac{{3T}}{4}\)đến T: Wđ giảm từ giá trị lớn nhất về 0 tại T, Wt tăng từ 0 đến giá trị lớn nhất tại T.
b) Tại thời điểm t = 0: Wđ = 0, Wt = W.
Tại thời điểm t = \(\frac{T}{8}\): Wđ = Wt = \(\frac{{\rm{W}}}{2}\).
Tại thời điểm t = \(\frac{T}{4}\): Wđ = W, Wt = 0.
Tại thời điểm t = \(\frac{{3T}}{8}\): Wđ = Wt = \(\frac{{\rm{W}}}{2}\).
→ ở mỗi thời điểm trên ta đều có: Wđ + Wt = W.



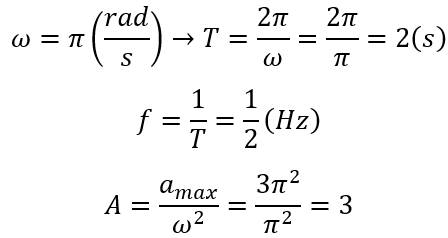
Thế năng của vật đạt giá trị lớn khi ở vị trí hai biên và đạt giá trị nhỏ nhất ở vị trí cân bằng khi vật di chuyển từ vị trí biên đến vị trí cân bằng thế năng của vật giảm dần từ giá trị lớn nhất về 0 và ngược lại.