Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Chứng minh:
\(d+d' =a \Rightarrow d' = a -d\)
Và \(f=\frac{d.d'}{d+d'} \Rightarrow d = \frac{d.(a-d)}{a}\)
\( \Rightarrow d^2 -ad + af =0\)
\( \Delta = a^2 -4af =a(a-4f)\)
(Điều kiện để phương trình có nghiệm là \(a \geq 4f \))
Vì đã có 1 ảnh rõ nét rồi nên phương trình sẽ có nghiệm, vì có vị trí thứ 2 nữa nên phương trình phải có 2 nghiệm phân biệt.
Ta có hai vị trí này là 2 nghiệm có phương trình:
\( d_1 = \frac{a+ \sqrt{\Delta}}{2}\)
\(d_2 = \frac{a- \sqrt{\Delta}}{2}\)
b) Gọi l =khoảng cách 2 vị trí trên ta có:
\( l = d_2 -d_1 = \frac{a+ \sqrt { \Delta} - (a- \sqrt { \Delta})}{2} = \sqrt{\Delta} \)
Ta có: \(l^2 = \Delta = a^2 -4af \Rightarrow f = \frac{a^2 -l^2 }{4a}\)
Để đo tiêu cự chỉ cần đo khoảng cách giữa 2 vị trị cho ảnh rõ nét trên màn và khoảng cách giữa vật- màn. Phương pháp này gọi là phương pháp Bessel. Hoặc có thể dùng bất đẳng thức Cauchy để chứng minh cũng được nhé!

Đáp án cần chọn là: D
Ta có công thức thấu kính:
1 d + 1 d ' = 1 f ⇒ 1 20 + 1 d ' = 1 10 ⇒ d ' = 20 c m

Đáp án: A
Vật thật cho ảnh cùng chiều, nhỏ hơn vật 2 lần nên ảnh là ảnh ảo và d’ = -6cm.
Theo công thức thấu kính và công thức số phóng đại:
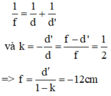
Đây là thấu kính phân kỳ.
Vị trí của vật để có ảnh nhỏ hơn vật 3 lần là d 2 , khi đó ta có:


Đáp án A
Vật thật cho ảnh cùng chiều, nhỏ hơn vật 2 lần nên ảnh là ảnh ảo và d’ = -6cm.
Theo công thức thấu kính và công thức số phóng đại:
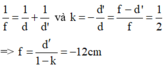
Đây là thấu kính phân kỳ.
Vị trí của vật để có ảnh nhỏ hơn vật 3 lần là d2, khi đó ta có:


Đáp án: C
Ảnh của vật cho bởi thấu kính cùng chiều và nhỏ hơn vật, nên ảnh là ảnh ảo và thấu kính phân kì.
Suy ra: d’ = -12m; d = 4│d’│=48cm
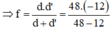

Đáp án C
Ảnh của vật cho bởi thấu kính cùng chiều và nhỏ hơn vật, nên ảnh là ảnh ảo và thấu kính phân kì
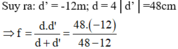

Khoảng cách từ ảnh đến thấu kính:
\(\dfrac{1}{f}=\dfrac{1}{d'}-\dfrac{1}{d}\Rightarrow\dfrac{1}{30}=\dfrac{1}{d'}-\dfrac{1}{10}\Rightarrow d'=7,5cm\)
Khoảng cách giữa vật và thấu kính:
\(d=10-7,58=2,5cm\)