Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Cứ 1 hạt nhân \(_{92}^{238}U\) bị phân rã tạo ra 1 hạt nhân \(_{82}^{206}Pb\). Từ đó ta có nhận xét là số hạt nhân \(_{92}^{238}U\) bị phân rã chính bằng số hạt nhân \(_{82}^{206}Pb\) tạo thành.
Tỉ số giữa số hạt nhân \(_{92}^{238}U\) bị phân rã và số hạt nhân \(_{92}^{238}U\) còn lại là
\(\frac{\Delta N}{N}= \frac{6,239.10^{18}}{1,188.10^{20}}= 0,0525 = \frac{1-2^{-\frac{t}{T}}}{2^{-\frac{t}{T}}}\)
Nhân chéo => \(2^{-\frac{t}{T}}= 0,95.\)
=> \(t = -T\ln_2 0,95 = 3,3.10^8\)(năm)
=> Tuổi của khối đã là 3,3.108 năm.

Đáp án C
Số hạt nhân con ở thời điểm t:
∆ N = N c o n = N 0 ( 1 - 2 - t T ) ⇔ m c o n A c o n . N A = m 0 A m e . N A ( 1 - 2 - t T )
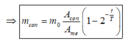
Áp dụng công thức ở trên ta được:

*Làm tròn đến chữ số thập phân thứ 3 thì m 0 = 0 , 867 g .

Cứ mỗi hạt nhân Pôlôni bị phân rã tạo thành 1 hạt nhân chì trong mẫu.
Số hạt nhân Pôlôni bị phân rã là \(\Delta N = N_0 2^{-\frac{t}{T}}.\)
Số hạt nhân Pônôni còn lại là \( N = N_0 2^{-\frac{t}{T}}.\)
Tại thời điểm t1 : \(\frac{\Delta N}{N } = \frac{1-2^{-\frac{t_1}{T}}}{2^{-\frac{t_1}{T}}}= \frac{1}{3}\)
=> \(3(1-2^{-\frac{t_1}{T}})= 2^{-\frac{t_1}{T}}\)
=> \(2^{-\frac{t_1}{T}}= 2^{-2}\)
=> \(t_1 = 2T\)
=> \(t_2 = 2T+276 = 552 \) (ngày)
=> \(\frac{t_2}{T}= \frac{552}{138}= 4.\)
Tại thời điểm t2 : \(\frac{\Delta N_1}{N_1 } = \frac{1-2^{-\frac{t_2}{T}}}{2^{-\frac{t_2}{T}}}= \frac{1-2^{-4}}{2^{-4}}= 15.\)
=> \(\frac{N_1}{\Delta N_1} = \frac{1}{15}.\)

Số hạt nhân chưa bị phân rã (số hạt nhân còn lại)
\(N= N_0 2^{-\frac{t}{T}} = N_02^{-\frac{0,5T}{T}}= N_02^{-0,5}= \frac{N_0}{\sqrt{2}}.\)

Kí hiệu \(N_{01}\), \(N_{02}\) là số hạt ban đầu lần lượt của \(^{235}U\) và \(^{238}U\).
t = 0 Ban đầu t thời điểm cần xác định hiện nay t 1 2
Hiện nay \(t_2\): \(\frac{N_{1}}{N_{2}}=\frac{N_{01}2^{-\frac{t_2}{T_1}}}{N_{02}2^{-\frac{t_2}{T_2}}} =\frac{7}{1000}.(1)\)
Thời điểm \(t_1\):
\(\frac{N_1}{N_2}= \frac{N_{01}2^{-\frac{t_1}{T_1}}}{N_{02}2^{-\frac{t_1}{T_2}}} = \frac{3}{100}.(2)\)
Chia (1) cho (2) => \(\frac{2^{-\frac{t_2}{T_1}}.2^{-\frac{t_1}{T_2}}}{2^{-\frac{t_1}{T_1}}.2^{-\frac{t_2}{T_2}}}= \frac{7.100}{3.1000}= \frac{7}{30}.\)
Áp dụng \(\frac{1}{2^{-x}} =2^x. \)
=> \(2^{(t_2-t_1)(\frac{1}{T_2}-\frac{1}{T_1})} = \frac{7}{30}.\)
=> \(t_2-t_1 = \frac{T_1T_2}{T_1-T_2}\ln_2 (7/30)=1,74.10^{9}\).(năm) \(= 1,74 \)(tỉ năm).
Như vậy cách hiện nay 1,74 tỉ năm thì trong urani tự nhiên có tỉ lệ số hạt thỏa mãn như bài cho.

Số hạt nhân chưa phóng xạ chính là số hạt nhân còn lại
\(N= N_0 2^{-\frac{t}{T}}= N_0 .2^{-4}= \frac{1}{16}N_0.\)
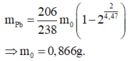
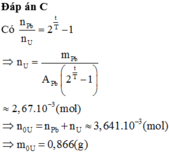
Đáp án C
Phương pháp:D Áp dụng công thức tính khối lượng chất mới sinh ra
Cách giải: Chọn C
Khối lượng Pb được tạo thành: