Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Vì khi (C) quay xung quanh trục nằm trong mặt phẳng chứa mạch thì khi đó góc giữ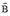a 
và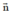 
thay đổi và làm từ thông qua mạch biến thiên.
Đáp án: D
f=B.v./q/.sin(B,v)=1.28.10-15N
e chuyển động thẳng đều=>vecto(f)+vecto(F từ)
=>vecto(f) cùng phương ngược chiều f từ và f=F từ
F từ=1,28.10-5N=>E=\(\dfrac{F}{q}\)=......(trị q)=8000V/m
vecto E hướng xuống
a/ \(\phi=N.BS\cos\left(\overrightarrow{B};\overrightarrow{n}\right)=200.10^{-4}.20.10^{-4}.\cos30^0=2\sqrt{3}.10^{-5}\left(T.m^2\right)\)
b/ \(E_c=\left|\frac{\Delta\phi}{\Delta t}\right|=\left|\frac{-2\sqrt{3}.10^{-5}}{0,01}\right|=2\sqrt{3}.10^{-3}\left(V\right)\)
\(Q=\frac{E_c^2}{R}t=\frac{\left(2\sqrt{3}.10^{-3}\right)^2}{10}.0,01=12.10^{-9}\left(J\right)\)
c/ \(I=\frac{E_c}{R+R'}=\frac{2\sqrt{3}.10^{-3}}{10+2}=\frac{\sqrt{3}.10^{-3}}{6}\left(A\right)\)
Check lại phần tính toán hộ mình nhé, nhiều số quá hơi nhức mắt :(
câu 1
giải
suất điện động cảm ứng
\(e_c=r.i=5.2=10V\)
mặt khác: \(e_c=\left|\frac{\Delta\Phi}{\Delta t}\right|=\frac{\Delta B}{\Delta t}.S\)
suy ra : \(\frac{\Delta B}{\Delta t}=\frac{e_c}{S}=\frac{10}{0,1^2}=10^3T/s\)
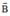
Đáp án D. Vì lưu huỳnh không phải là vật dẫn.