

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Đáp án A
Cường độ dòng điện hiệu dụng được định nghĩa trên công suất tỏa nhiệt trung bình của dòng điện này trong một chu kì.
Trong một phần ba đầu của chu kì thì i=1A nhiệt lượng tỏa ra trong thời gian này là ![]() .
.
Trong hai phần ba sau của chu kì thì i=-2 Anhiệt lượng tỏa ra trong thời gian này là ![]()
→ Nhiệt lượng tỏa ra trong một chu kì là 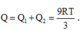
Công suất tỏa nhiệt trung bình của dòng điện trong một chu kì là P= Q/T= 3R
Mà ![]()

Mạch chỉ có điện trở thuần thì u cùng pha với i.
Nếu \(u=U_0\cos\left(\omega t+\varphi\right)\)
Thì: \(i=I_0\cos\left(\omega t+\varphi\right)\)
\(\Rightarrow\frac{u}{U_0}=\frac{i}{I_0}\)
\(\Rightarrow\frac{u^2}{U_0^2}+\frac{i^2}{I_0^2}=1\) là sai.

\(U_{RC}=const=U\) khi \(Z_{L1}=2Z_C=R\)
Mặt khác L thay đổi để : \(U_{Lmax}:U_{Lmax}=\frac{U\sqrt{R^2+Z^2_C}}{R}=\frac{U\sqrt{2^2+1}}{2}=\frac{U\sqrt{5}}{2}\)
\(\Rightarrow chọn.D\)
+,có C=C1=>U_R=\frac{U.R}{\sqrt{R^2+(Zl-ZC1)^2}}
+,U R ko đổi =>Zl=ZC1
+,có c=C1/2=>ZC=2ZC1
=>U(AN)=U(RL)=\frac{U\sqrt{r^2+Z^2l}}{\sqrt{R^2+(Zl-2Z^2C1)}}=u=200V

Ta có:
Trong 1 (s) ứng với 50 chu kì mà mỗi chu kì có độ lớn 1 (A) 4 lần
⇒ 50 chu lì có 50.4 = 200 (lần)


Bạn cần tìm vị trí li độ ứng với t = 1/200 thì thay vào hàm i => i =2(VTBiên dương) ở vị trí B như hình vẽ.
Tương tự thay t = 0.015 vào i => i = -2 (VTBiên âm).C
Có 1 vị trí có giá trị \(A\sqrt{2}\) như hình vẽ
Tìm góc quay được \(\cos\varphi_1=\frac{A\sqrt{2}}{A}=\sqrt{2}\Rightarrow\varphi_1=\frac{\pi}{4}.\)
=> Thời gian quay ứng với góc phi 1 là \(t=\frac{\varphi_1}{\omega}=0.0025s.\)
Như vậy thời điểm vật ở li độ \(A\sqrt{2}\) là \(t_M=t_1+t=\frac{1}{200}+0.0025=0.0075s.\)

Đáp án C.
lúc đầu ta có :
UMB=2UR => ZMB=2R <=> ZC=\(\sqrt{3}\)R mà C=\(\frac{L}{R^2}\) => ZL=\(\frac{R}{\sqrt{3}}\)
lúc sau ta có Uc' max :
Zc'.ZL=R2+ \(Z^2_L\) => Zc'=\(\frac{4R}{\sqrt{3}}\)
\(\text{tanφ}=\frac{Z_L-Z_C}{R}\Rightarrow\tan\varphi=-\sqrt{3}\Rightarrow\varphi=-\frac{\pi}{3}\)

Sử dụng đường tròn
Từ thời điểm 0-0.01 s thì góc quay được là \(\varphi = 0.01.\omega = \pi (rad).\)
I 0 π/3 t=0 M N I 0 2 I 0 2 - t=0.01 P Q t 1 t 2 π/6 φ1 φ2
Thời điểm t =0 ứng với điểm M; thời điểm t = 0.01s ứng với điểm N. Từ M đến N sẽ qua hai điểm P và Q có giá trị (độ lớn) 0.5I0.
tại P: \(\varphi_1 = t_1 \omega => t_1 = \frac{\pi/3}{100\pi} = \frac{1}{300}s\)
tại Q: \(\varphi_2 = t_2 \omega => t_2 = \frac{\pi/3+\pi/6+\pi/6}{100\pi} = \frac{2}{300}s\)
chọn đáp án. A