Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Mạch chỉ có điện trở thuần thì u cùng pha với i.
Nếu \(u=U_0\cos\left(\omega t+\varphi\right)\)
Thì: \(i=I_0\cos\left(\omega t+\varphi\right)\)
\(\Rightarrow\frac{u}{U_0}=\frac{i}{I_0}\)
\(\Rightarrow\frac{u^2}{U_0^2}+\frac{i^2}{I_0^2}=1\) là sai.

\(U_{RC}=const=U\) khi \(Z_{L1}=2Z_C=R\)
Mặt khác L thay đổi để : \(U_{Lmax}:U_{Lmax}=\frac{U\sqrt{R^2+Z^2_C}}{R}=\frac{U\sqrt{2^2+1}}{2}=\frac{U\sqrt{5}}{2}\)
\(\Rightarrow chọn.D\)
+,có C=C1=>U_R=\frac{U.R}{\sqrt{R^2+(Zl-ZC1)^2}}
+,U R ko đổi =>Zl=ZC1
+,có c=C1/2=>ZC=2ZC1
=>U(AN)=U(RL)=\frac{U\sqrt{r^2+Z^2l}}{\sqrt{R^2+(Zl-2Z^2C1)}}=u=200V

Công suất tiêu thụ của mạch gồm R và r là:
\(P=I^2\left(R+r\right)\)

Đáp án C.
lúc đầu ta có :
UMB=2UR => ZMB=2R <=> ZC=\(\sqrt{3}\)R mà C=\(\frac{L}{R^2}\) => ZL=\(\frac{R}{\sqrt{3}}\)
lúc sau ta có Uc' max :
Zc'.ZL=R2+ \(Z^2_L\) => Zc'=\(\frac{4R}{\sqrt{3}}\)
\(\text{tanφ}=\frac{Z_L-Z_C}{R}\Rightarrow\tan\varphi=-\sqrt{3}\Rightarrow\varphi=-\frac{\pi}{3}\)

Bạn nên gửi mỗi câu hỏi một bài thôi để mọi người tiện trao đổi.
1. \(Z_L=200\sqrt{3}\Omega\), \(Z_C=100\sqrt{3}\Omega\)
Suy ra biểu thức của i: \(i=1,1\sqrt{2}\cos\left(100\pi t-\frac{\pi}{3}\right)A\)
Công suất tức thời: p = u.i
Để điện áp sinh công dương thì p > 0, suy ra u và i cùng dấu.
Biểu diễn vị trí tương đối của u và i bằng véc tơ quay ta có:
u u i i 120° 120°
Như vậy, trong 1 chu kì, để u, i cùng dấu thì véc tơ u phải quét 2 góc như hình vẽ.
Tổng góc quét: 2.120 = 2400
Thời gian: \(t=\frac{240}{360}.T=\frac{2}{3}.\frac{2\pi}{100\pi}=\frac{1}{75}s\)
2. Khi nối tắt 2 đầu tụ điện thì cường độ dòng điện hiệu dụng không đổi \(\Rightarrow Z_1=Z_2\Leftrightarrow Z_C-Z_L=Z_L\Leftrightarrow Z_C=2Z_L\)
\(U_C=1,2U_d\Leftrightarrow Z_C=2Z_d\Leftrightarrow Z_C=2\sqrt{R^2+Z_L^2}\)
\(\Leftrightarrow2Z_L=\sqrt{R^2+Z_L^2}\Leftrightarrow R=\sqrt{3}Z_L\)
Khi bỏ tụ C thì cường độ dòng điện của mạch là: \(I=\frac{U}{Z_d}=\frac{U}{\sqrt{R^2+Z_L^2}}=\frac{220}{\sqrt{3.Z_L^2+Z_L^2}}=0,5\)
\(\Rightarrow Z_L=220\Omega\)

\(I_0 = q_0.\omega = 4.10^{-12}.10^7= 4.10^{-5}A.\)
\(\left(\frac{q}{q_0}\right)^2+\left(\frac{i}{I_0}\right)^2=1\)
=> \(\left(\frac{i}{I_0}\right)^2=1-\left(\frac{q}{q_0}\right)^2 = 1 - \left(\frac{2.10^{-12}}{4.10^{-12}}\right)^2= \frac{3}{4}.\)
=> \(i = I_0.\frac{\sqrt{3}}{2}=2\sqrt{3}.10^{-5}A.\)
Do u vuông pha với i nên áp dụng công thức độc lập thời gian:
\((\dfrac{u}{U_0})^2+(\dfrac{i}{I_0})^2=1\)


Đáp án A
Cường độ dòng điện hiệu dụng được định nghĩa trên công suất tỏa nhiệt trung bình của dòng điện này trong một chu kì.
Trong một phần ba đầu của chu kì thì i=1A nhiệt lượng tỏa ra trong thời gian này là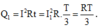 .
.
Trong hai phần ba sau của chu kì thì i=-2 Anhiệt lượng tỏa ra trong thời gian này là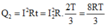
→ Nhiệt lượng tỏa ra trong một chu kì là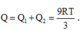
Công suất tỏa nhiệt trung bình của dòng điện trong một chu kì là P= Q/T= 3R
Mà