Đồ thị li độ của một vật dao động điều hòa có dạng như hình vẽ. Phương trình dao động của vật là <img src="http://cdn.hoc24.vn/bk/ebC4M7AhcoEn.png" alt="" width="218" heigh...

Đồ thị li độ của một vật dao động điều hòa có dạng như hình vẽ. Phương trình dao động của vật là

Khách

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Mua vip

Hoàng Đức Long

2 tháng 4 2017

Đồ thị li độ của một vật dao động điều hòa có dạng như hình vẽ. Phương trình dao động của vật là

A. $x = 4 \cos \frac{π}{3} (t - \frac{π}{3}) c m$

B. $x = 4 \cos \frac{π}{3} (t - 1) c m$

C. $x = 4 \cos (2 πt - \frac{π}{6}) c m$

D. $x = 4 \cos (\frac{2 π}{7} t - \frac{π}{6}) c m$

#Hỏi cộng đồng OLM #Vật lý lớp 11

Vũ Thành Nam

2 tháng 4 2017

Đúng(0)

Các câu hỏi dưới đây có thể giống với câu hỏi trên

Almoez Ali

15 tháng 10 2023

Một vật dao động điều hòa theo phương trình x = 10cos(πt + π/3 ) (cm/s). Kể từ lúc t = 0 thời điểm vận tốc của vật có độ lớn 5π (cm/s) lần thứ 21 là:

#Hỏi cộng đồng OLM #Vật lý lớp 11

2611

18 tháng 10 2023

Trong `5` chu kì vật đi qua thời điểm vận tốc có độ lớn `5\pi(cm//s)` là `20` lần.

`=>1` lần vật đi trong: `\Delta t=T/12+T/6=T/4`

`=>` Kể từ `t=0` thời điểm vận tốc của vật có độ lớn `5\pi(cm//s)` lần thứ `21` là:

`t=T/4+5T=10,5(s)`.

Đúng(0)

Nguyễn Văn Hà Bách

5 tháng 9 2021 - olm

một con lắc lò xo gồm vật nặng có khối lượng 10g gắn với lò xo có độ cứng 10N/m dao động điều hòa trên mặt sàn nhẵn nằm ngang với phương trình x=10cos ωt (cm), vào thời điểm t vật chịu tác dụng của lực F hướng dọc theo trục của lò xo và có độ lớn không đổi F=0,6N sau thời điểm đó vật dao động trên quỹ đạo có chiều dài 16cm. Vật bắt đầu chịu tác dụng của lực F khi nó...

Đọc tiếp

#Hỏi cộng đồng OLM #Vật lý lớp 11

Nguyễn Văn Quang

22 tháng 10 2023 - olm

Một vật dao động điều hòa dọc theo trục Ox với phương trình vận tốc là overline v = 16π cos(4πt - π/6) cm/ s . Xác định thời điểm lần thứ 2023 vật chuyển động nhanh dần qua vị trí x =2 kể từ lúc bắt đầu dao động

#Hỏi cộng đồng OLM #Vật lý lớp 11

Lê Song Phương

22 tháng 10 2023

Từ pt $v=16\pi\cos\left(4\pi t-\dfrac{\pi}{6}\right)=16\pi\cos\left(4\pi t-\dfrac{2\pi}{3}+\dfrac{\pi}{2}\right)$ (cm/s), ta suy ra $\omega=4\pi\left(rad/s\right)$, lại có $\omega A=16\pi\Leftrightarrow A=\dfrac{16\pi}{\omega}=4\left(cm\right)$

$\varphi_0=-\dfrac{2\pi}{3}$; $T=\dfrac{2\pi}{\omega}=0,5\left(s\right)$

Đường tròn lượng giác:

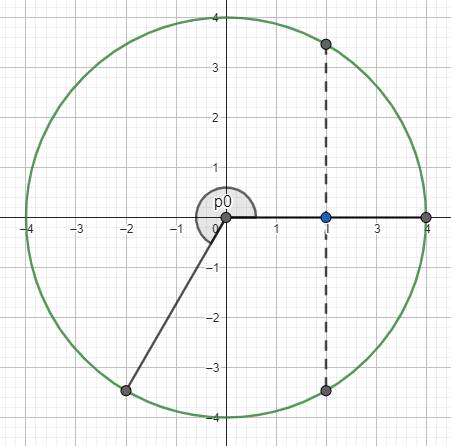
Từ đây, ta có thể thấy tại thời điểm lần thứ 2023 vật chuyển động qua vị trí $x=2$ kể từ khi dao động, góc quét của vật là $\Delta\varphi=\dfrac{\pi}{3}+1011.2\pi=\dfrac{6067}{3}\pi$ (rad)

Thời điểm lần thứ 2023 vật chuyển động qua vị trí $x=2$ kể từ lúc bắt đầu dao động là $\Delta t=\dfrac{\Delta\varphi}{2\pi}.T=\dfrac{\dfrac{6067}{3}\pi}{2\pi}.0,5=\dfrac{6067}{12}\approx505,58\left(s\right)$

Đúng(1)

Vi Nguyễn

7 tháng 11 2023

Một chất điểm dao động điều hòa có phương trình x=2cos(5πt-π/4) (cm) a) Xác định biên độ, chu kì, tần số và chiều dài quỹ đạo của dao động. b) Viết phương trình vận tốc và gia tốc của chất điểm. c) Tính pha, li độ, vận tốc và gia tốc ở thời điểm t = 0,2 s.

#Hỏi cộng đồng OLM #Vật lý lớp 11

nguyễn thị hương giang

8 tháng 11 2023

Phương trình: $x=2cos\left(5\pi t-\dfrac{\pi}{4}\right)$

a)Biên độ: $A=2cm$

Chu kì: $T=\dfrac{2\pi}{\omega}=\dfrac{2\pi}{5\pi}=0,4s$

Tần số: $f=\dfrac{1}{T}=\dfrac{1}{0,4}=2,5Hz$

Chiều dài quỹ đạo: $L=2A=2\cdot2=4cm$

b)Phương trình chất điểm:

Vận tốc: $v=-\omega Asin\left(\omega t+\varphi\right)=-10\pi sin\left(5\pi t-\dfrac{\pi}{4}\right)$

Gia tốc: $a=-\omega^2Acos\left(\omega t+\varphi\right)=-500cos\left(5\pi t-\dfrac{\pi}{4}\right)$

c)Em thay giá trị $t=0,2s$ vào từng pt nhé.

Đúng(1)

Vi Nguyễn

20 tháng 12 2023

Tại sao gia tốc lại bằng 250căn2 loading...

Đúng(0)

Chy Nguyen

12 tháng 8 - olm

x=8cos(5πt+ π/3)a. Xác định trạng thái đầub. Xác định thời điểm lần đầu vật đạt vị trí biên dươngc. Xác định thời điểm lần đầu vật qua vị trí cân bằngd. Xác định thời điểm lần thứ 5 vật qua vị trí x=-4cm,...

Đọc tiếp

#Hỏi cộng đồng OLM #Vật lý lớp 11

Trần Hoàng Trung

VIP

11 giờ trước (18:53)

Ta có phương trình dao động điều hòa của vật:

$x = 8 cos ⁡ \left(\right. 5 \pi t + \frac{\pi}{3} \left.\right)$

Trong đó:

$x$ là vị trí của vật (đơn vị cm),
$t$ là thời gian (đơn vị s),
$8$ là biên độ dao động (đơn vị cm),
$5 \pi$ là tần số góc (rad/s),
$\frac{\pi}{3}$ là pha ban đầu.

Chúng ta sẽ lần lượt giải quyết từng câu hỏi.

a. Xác định trạng thái đầu

Trạng thái đầu của vật là trạng thái tại thời điểm $t = 0$.

Thay $t = 0$ vào phương trình dao động:

$x \left(\right. 0 \left.\right) = 8 cos ⁡ \left(\right. 5 \pi \times 0 + \frac{\pi}{3} \left.\right) = 8 cos ⁡ \left(\right. \frac{\pi}{3} \left.\right)$

Biết rằng $cos ⁡ \left(\right. \frac{\pi}{3} \left.\right) = \frac{1}{2}$, ta có:

$x \left(\right. 0 \left.\right) = 8 \times \frac{1}{2} = 4 \textrm{ } \text{cm}$

Vậy, trạng thái đầu của vật là $x = 4 \textrm{ } \text{cm}$.

b. Xác định thời điểm lần đầu vật đạt vị trí biên dương

Vị trí biên dương là giá trị cực đại của $x$, tức là khi $x = 8 \textrm{ } \text{cm}$ (biên độ dao động).

Ta cần tìm thời điểm $t$ sao cho:

$8 cos ⁡ \left(\right. 5 \pi t + \frac{\pi}{3} \left.\right) = 8$

Chia hai vế cho 8:

$cos ⁡ \left(\right. 5 \pi t + \frac{\pi}{3} \left.\right) = 1$

Giải phương trình:

$5 \pi t + \frac{\pi}{3} = 2 k \pi \text{v}ớ\text{i} \textrm{ } k \in \mathbb{Z}$

Giải phương trình trên:

$5 \pi t = 2 k \pi - \frac{\pi}{3}$

Chia cả hai vế cho $5 \pi$:

$t = \frac{2 k \pi - \frac{\pi}{3}}{5 \pi} = \frac{2 k - \frac{1}{3}}{5}$

Khi $k = 0$, ta có:

$t = \frac{- \frac{1}{3}}{5} = - \frac{1}{15} \textrm{ } \text{s}$

Vì thời gian phải dương, ta chọn $k = 1$:

$t = \frac{2 - \frac{1}{3}}{5} = \frac{\frac{5}{3}}{5} = \frac{1}{3} \textrm{ } \text{s}$

Vậy, thời điểm lần đầu vật đạt vị trí biên dương là $t = \frac{1}{3} \textrm{ } \text{s}$.

c. Xác định thời điểm lần đầu vật qua vị trí cân bằng

Vị trí cân bằng là $x = 0$, tức là khi $cos ⁡ \left(\right. 5 \pi t + \frac{\pi}{3} \left.\right) = 0$.

Ta giải phương trình:

$cos ⁡ \left(\right. 5 \pi t + \frac{\pi}{3} \left.\right) = 0$

Điều này xảy ra khi:

$5 \pi t + \frac{\pi}{3} = \frac{\pi}{2} + k \pi \text{v}ớ\text{i} \textrm{ } k \in \mathbb{Z}$

Giải phương trình:

$5 \pi t = \frac{\pi}{2} + k \pi - \frac{\pi}{3}$

Tính toán:

$5 \pi t = \frac{\pi}{6} + k \pi$

Chia cả hai vế cho $5 \pi$:

$t = \frac{\frac{\pi}{6} + k \pi}{5 \pi} = \frac{1}{30} + \frac{k}{5}$

Khi $k = 0$, ta có:

$t = \frac{1}{30} \textrm{ } \text{s}$

Vậy, thời điểm lần đầu vật qua vị trí cân bằng là $t = \frac{1}{30} \textrm{ } \text{s}$.

d. Xác định thời điểm lần thứ 5 vật qua vị trí $x = - 4 \textrm{ } \text{cm}$, với $v > 0$

Vị trí $x = - 4 \textrm{ } \text{cm}$ ứng với phương trình:

$- 4 = 8 cos ⁡ \left(\right. 5 \pi t + \frac{\pi}{3} \left.\right)$

Chia hai vế cho 8:

$- \frac{1}{2} = cos ⁡ \left(\right. 5 \pi t + \frac{\pi}{3} \left.\right)$

Giải phương trình:

$5 \pi t + \frac{\pi}{3} = \pi - \frac{\pi}{3} + 2 k \pi \text{v}ớ\text{i} \textrm{ } k \in \mathbb{Z}$

Tính toán:

$5 \pi t + \frac{\pi}{3} = \frac{2 \pi}{3} + 2 k \pi$$5 \pi t = \frac{2 \pi}{3} + 2 k \pi - \frac{\pi}{3} = \frac{\pi}{3} + 2 k \pi$

Chia cả hai vế cho $5 \pi$:

$t = \frac{\frac{\pi}{3} + 2 k \pi}{5 \pi} = \frac{1}{15} + \frac{2 k}{5}$

Vậy:

$t_{1} = \frac{1}{15} \textrm{ } \text{s} \left(\right. k = 0 \left.\right)$$t_{2} = \frac{7}{15} \textrm{ } \text{s} \left(\right. k = 1 \left.\right)$$t_{3} = \frac{13}{15} \textrm{ } \text{s} \left(\right. k = 2 \left.\right)$$t_{4} = \frac{19}{15} \textrm{ } \text{s} \left(\right. k = 3 \left.\right)$$t_{5} = \frac{25}{15} = \frac{5}{3} \textrm{ } \text{s} \left(\right. k = 4 \left.\right)$

Vậy, thời điểm lần thứ 5 vật qua vị trí $x = - 4 \textrm{ } \text{cm}$ với $v > 0$ là $t = \frac{5}{3} \textrm{ } \text{s}$.

Tóm tắt:

a. Trạng thái đầu: $x = 4 \textrm{ } \text{cm}$
b. Thời điểm lần đầu vật đạt vị trí biên dương: $t = \frac{1}{3} \textrm{ } \text{s}$
c. Thời điểm lần đầu vật qua vị trí cân bằng: $t = \frac{1}{30} \textrm{ } \text{s}$
d. Thời điểm lần thứ 5 vật qua vị trí $x = - 4 \textrm{ } \text{cm}$ với $v > 0$: $t = \frac{5}{3} \textrm{ } \text{s}$

Đúng(0)

Trần Hoàng Trung

VIP

11 giờ trước (18:54)

Tham khảo

Đúng(0)

Hoàng Đức Long

23 tháng 2 2019

Một chất điểm dao động điều hòa trên trục Ox với biên độ 10 cm. Hình vẽ là đồ thị phụ thuộc thời gian của pha dao động (dạng hàm cos). Phương trình dao động của vật là A. x = 10cos(πt - π/3) cm B. x = 10cos(2πt - π/3) cm C. x = 10cos(πt + π/3) cm D. x = 10cos(2πt + π/3) cm...

Đọc tiếp

#Hỏi cộng đồng OLM #Vật lý lớp 11

Vũ Thành Nam

23 tháng 2 2019

Chọn C

Đúng(0)

Ân Lan Khắc

6 tháng 7 2023 - olm

1. Một chất điểm dao động điều hòa có phương trình li độ theo thời gian là x= 5$\sqrt{3}$ cos(10$\pi$t + $\dfrac{\pi}{3}$ )(cm) . Tần số của dao động bằng: A. 10Hz B. 20Hz C. 10$\pi$Hz D. 5Hz 2. Một chất điểm dao động điều hòa có phương trình li độ theo thời gian là x= 6cos(4$\pi$t + $\dfrac{\pi}{3}$ ) (cm) . chu kì của dao động bằng: A. 4s B. 2s ...

Đọc tiếp

#Hỏi cộng đồng OLM #Vật lý lớp 11

nguyễn thanh

21 tháng 9 2023

một vật dao đông điều hòa với phương trình x=10cos(5πt+π/3).xác định li độ và vận tốc tại thời điểm t=1/15 s

#Hỏi cộng đồng OLM #Vật lý lớp 11

Hà Quang Minh

Giáo viên

21 tháng 9 2023

Ta có: $x=10cos\left(5\pi\cdot\dfrac{1}{15}+\dfrac{\pi}{3}\right)=-5\\ v=x'=-50\pi sin\left(5\pi\cdot\dfrac{1}{15}+\dfrac{\pi}{3}\right)=-25\pi\sqrt{3}$

Đúng(1)

Almoez Ali

15 tháng 10 2023

Vật dao động điều hòa theo phương trình : x = 4cos(π.t - π/6) cm .Thời gian ngắn nhất vật đi từ vị trí có li độ x1=−2√2 cm đến vị trí có li độ x2 = 2√3 cm theo chiều âm là :

#Hỏi cộng đồng OLM #Vật lý lớp 11

YuanShu

15 tháng 10 2023

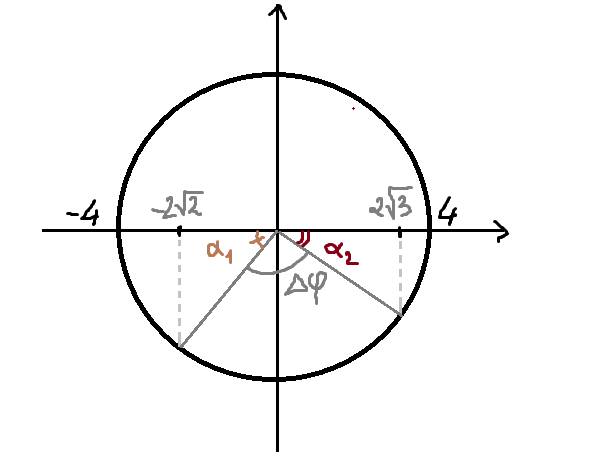
Ta có : $A=4cm$

$cos\alpha_1=\dfrac{-2\sqrt{2}}{4}=-\dfrac{\sqrt{2}}{2}\Rightarrow\alpha_1=\dfrac{3\pi}{4}rad$

$cos\alpha_2=\dfrac{2\sqrt{3}}{4}=\dfrac{\sqrt{3}}{2}\Rightarrow\alpha_2=\dfrac{\pi}{6}rad$

$\Delta\varphi=\left(\dfrac{\pi}{2}-\dfrac{3\pi}{4}\right)+\left(\dfrac{\pi}{2}-\dfrac{\pi}{6}\right)=\dfrac{\pi}{12}rad$

Có : $T=\dfrac{2\pi}{\omega}=\dfrac{2\pi}{\pi}=2s$

$\Delta t=\dfrac{\Delta\varphi}{2\pi}.T=\dfrac{\dfrac{\pi}{12}}{2\pi}.2=\dfrac{1}{12}s$

Vậy ...

Hình ảnh biểu diễn :

Đúng(2)

a. Xác định trạng thái đầu

b. Xác định thời điểm lần đầu vật đạt vị trí biên dương

c. Xác định thời điểm lần đầu vật qua vị trí cân bằng

d. Xác định thời điểm lần thứ 5 vật qua vị trí \(x = - 4 \textrm{ } \text{cm}\), với \(v > 0\)

Tóm tắt:

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

a. Xác định trạng thái đầu

b. Xác định thời điểm lần đầu vật đạt vị trí biên dương

c. Xác định thời điểm lần đầu vật qua vị trí cân bằng

d. Xác định thời điểm lần thứ 5 vật qua vị trí \(x = - 4 \textrm{ } \text{cm}\), với \(v > 0\)

Tóm tắt:

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP