Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi x (cm) là độ dài cạnh AC (x > 2).
Gọi hình chữ nhật là MNPA như hình vẽ.
Ta có: MC = AC – AM = x – 2 (cm)
Vì MN // AB nên theo định lý Talet ta có tỉ lệ:
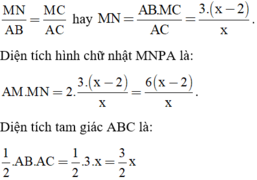
Vì diện tích tam giác ABC gấp đôi diện tích hình chữ nhật MNPA nên ta có phương trình:
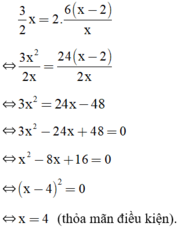
Vậy độ dài đoạn thẳng AC là 4cm.

3\(a^2\)+4a+1=3\(a^2\)+3a+a+1
=(3\(a^2\)+3a)+(a+1)
=3a(a+1)+(a+1)
=(a+1)(3a+1)

Bài 1)
a) Tứ giác AIHK có 3 góc vuông \(\widehat{HKA}=\widehat{HIA}=\widehat{KAI}=90^0\)
Nên suy ra góc còn lại cũng vuông.Tứ giác có 4 góc vuông là hình chữ nhật
b) Câu này không đúng rồi bạn
Nếu thực sự hai tam giác kia đồng dạng thì đầu bài phải cho ABC vuông cân
Vì nếu góc AKI = góc ABC = 45 độ ( IK là đường chéo đồng thời là tia phân giác của hình chữ nhật)
c) Ta có : Theo hệ thức lượng trong tam giác ABC vuông
\(AB^2=BC.BH=13.4\)
\(\Rightarrow AB=2\sqrt{13}\)
\(AC=\sqrt{9\cdot13}=3\sqrt{13}\)
Vậy \(S_{ABC}=\frac{AB\cdot AC}{2}=\frac{6\cdot13}{2}=39\left(cm^2\right)\)
Bài 2)
a) \(ED=AD-AE=17-8=9\)
Xét tỉ lệ giữa hai cạnh góc vuông trong hai tam giác ABE và DEC ta thấy
\(\frac{AB}{AE}=\frac{ED}{DC}\Leftrightarrow\frac{6}{8}=\frac{9}{12}=\frac{3}{4}\)
Vậy \(\Delta ABE~\Delta DEC\)
b) \(\frac{S_{ABE}}{S_{DEC}}=\frac{AB\cdot AE\cdot\frac{1}{2}}{DE\cdot DC\cdot\frac{1}{2}}=\frac{6\cdot8}{9\cdot12}=\frac{4}{9}\)
c) Kẻ BK vuông góc DC.Suy ra tứ giác ABKD là hình chữ nhật vì có 4 góc vuông
Nên BK = AD và AB = DK
\(\Rightarrow KC=DC-DK=12-6=6\)
Theo định lý Pytago ta có
\(BC=\sqrt{BK^2+KC^2}=\sqrt{17^2+6^2}=5\sqrt{13}\)

A B C M D E 8 6
a) ADME là hình gì?
tứ giác ADME có:
\(\widehat{A}=90^o\)(Tam giác ABC vuông tại A)
\(\widehat{MDA}=90^o\)(\(MD\perp AB\))
\(\widehat{MEA}=90^o\)(\(ME\perp AC\))
Suy ra ADME là hình chữ nhật.
b) Tìm điều kiện của tam giác ABC để ADME là hình vuông
Hình chữ nhật ADME là hình vuông
\(\Leftrightarrow\)AM là phân giác \(\widehat{DAE}\)hay AM là phân giác \(\widehat{BAC}\)
mà AM là trung tuyến của tam giác vuông ABC
\(\Rightarrow\Delta ABC\)vuông cân tại A.
c) tính AM?
Áp dụng định lý pytago vào tam giác ABC
có \(BC^2=AB^2+AC^2=6^2+8^2=100\)
\(\Rightarrow BC=\sqrt{100}=10\left(cm\right)\)
Vì AM là đường trung tuyến ứng với cạnh huyền BC của tam giác vuông ABC nên \(AM=\frac{BC}{2}=\frac{10}{2}=5\left(cm\right)\)
d) Tính \(S_{ABM}\)?
tam giác ABC có M trung điểm BC mà ME // AD (ADME hình chữ nhật) hay ME // AB
=> ME là đường trung bình tam giác ABC
=> E trung điểm AC
\(\Rightarrow AE=\frac{AC}{2}=\frac{6}{2}=3\left(cm\right)\)
mà DM = AE (ADME là hcn)
\(\Rightarrow AE=DM=3\left(cm\right)\)
\(\Rightarrow S_{ABM}=\frac{1}{2}.AB.DM=\frac{1}{2}.8.3=12\left(cm^2\right)\)
ĐS:...........
(Thời gian hoàn thành 9:37 PM)
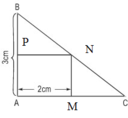

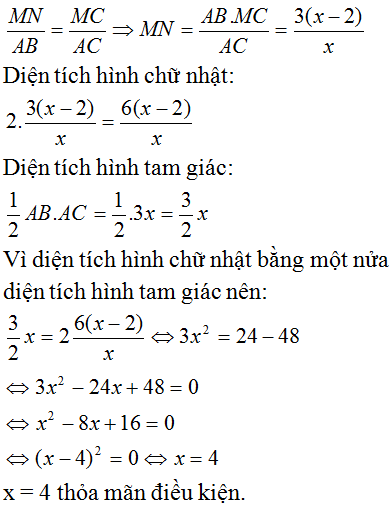
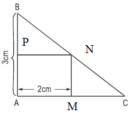
Đáp án B
Gọi x (cm) là độ dài cạnh AC (x > 2).
Gọi hình chữ nhật là MNPA như hình vẽ.
Ta có: MC = AC – AM = x – 2 (cm)
Vì MN // AB nên theo định lý Talet ta có tỉ lệ:
Vì diện tích tam giác ABC gấp đôi diện tích hình chữ nhật MNPA nên ta có phương trình:
Vậy độ dài đoạn thẳng AC là 4cm.