Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài giải:
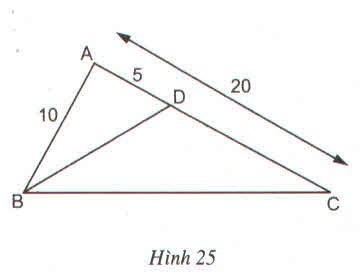
a) Góc ngoài còn lại: 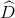 =3600 – (750 + 900 + 1200) = 750
=3600 – (750 + 900 + 1200) = 750
Ta tính được các góc ngoài tại các đỉnh A, B, C, D lần lượt là:
1050, 900, 600, 1050
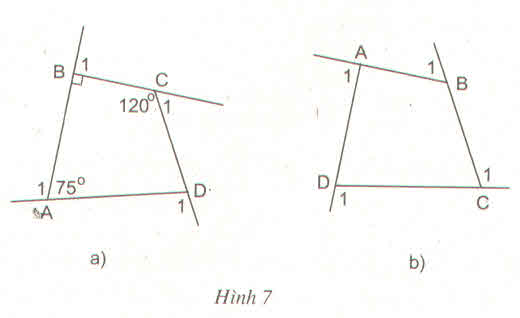
b)Hình 7b SGK:
Tổng các góc trong  +
+  +
+ +
+ =3600
=3600
Nên tổng các góc ngoài
 +
+  +
+ +
+ =(1800 -
=(1800 -  ) + (1800 -
) + (1800 -  ) + (1800 -
) + (1800 -  ) + (1800 -
) + (1800 -  )
)
=(1800.4 - ( 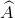 +
+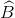 +
+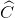 +
+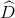 )
)
=7200 – 3600 =3600
c) Nhận xét: Tổng các góc ngoài của tứ giác bằng 3600
Xét tứ giác ABCD có:
\(\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360^o\)
\(\Leftrightarrow\widehat{D}=360^o-\left(\widehat{A}+\widehat{B}+\widehat{C}\right)\)
\(\Leftrightarrow\widehat{D}=360^o-\left(90^o+120^o+75^o\right)\)
\(\Leftrightarrow\widehat{D}=360^o-285^o=75^o\)
Ta có:+)\(\widehat{BAD}+\widehat{A_1}=180^o\) (hai góc kề bù)
\(\Rightarrow\widehat{A_1}=180^o-\widehat{BAD}\)
\(\Rightarrow\widehat{A_1}=180^o-75^o=105^o\)
+)\(\widehat{B}_1+\widehat{CBA}=180^o\) (hai góc kề bù)
\(\Rightarrow\widehat{B_1}=180^o-\widehat{CBA}\)
\(\Rightarrow\widehat{B_1}=180^o-90^0=90^o\)
\(+)\widehat{C_1}+\widehat{BCD}=180^o\) (hai góc kề bù)
\(\Rightarrow\widehat{C_1}=180^o-\widehat{BCD}\)
\(\Rightarrow\widehat{C_1}=180^o-120^o=60^o\)
\(+)\widehat{D_1}+\widehat{ADC}=180^o\) (hai góc kề bù)
\(\Rightarrow\widehat{D}_1=180^o-\widehat{ADC}\)
\(\Rightarrow\widehat{D_1}=180^o-75^o=105^o\)
b,Xét tứ giác ABCD có:
\(\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360^o\)
\(\widehat{A_1}+\widehat{B_1}+\widehat{C_1}+\widehat{D_1}\)
\(=\left(180^o-\widehat{A}\right)+\left(180^o-\widehat{B}\right)+\left(180^o-\widehat{C}\right)+\left(180^o-\widehat{D}\right)\)
\(=180^o.4-\left(\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}\right)\)
\(=720^o-360^o=360^o\)
c) Nhận xét: Tổng các góc ngoài của tứ giác bằng \(360^o\)

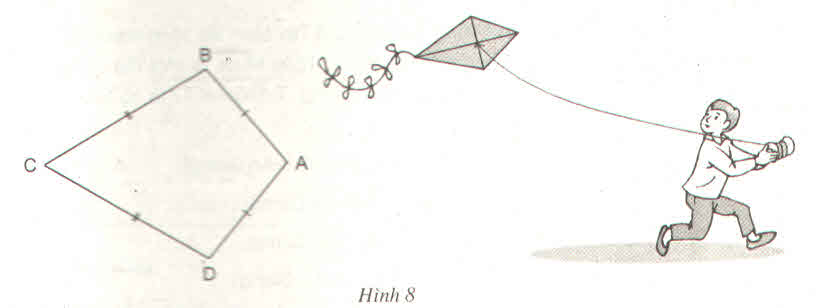
a) Ta có: AB = AD (gt) => A thuộc đường trung trực của BD
CB = CD (gt) => C thuộc đường trung trực của BD.
Vậy AC là đường trung trực của BD.
b) Xét ∆ ABC và ∆ADC có AB = AD (gt)
BC = DC (gt)
AC cạnh chung
nên ∆ ABC = ∆ADC (c.c.c)

Suy ra: ⇒ \(\widehat{B}=\widehat{D}\)
Ta có \(\widehat{B}+\widehat{D}=360^o-\left(100^o+60^o\right)=200^o\)
Do đó \(\widehat{B}=\widehat{D}=100^o\)
Bài giải:
a) Ta có: AB = AD (gt) => A thuộc đường trung trực của BD
CB = CD (gt) => C thuộc đường trung trực của BD.
Vậy AC là đường trung trực của BD.
b) Xét ∆ ABC và ∆ADC có AB = AD (gt)
BC = DC (gt)
AC cạnh chung
nên ∆ ABC = ∆ADC (c.c.c)

Suy ra: ⇒ˆB=ˆD⇒B^=D^
Ta có ˆB+ˆD=3600−(100+60)=200B^+D^=3600−(100+60)=200
Do đó ˆB=ˆD=1000B^=D^=1000

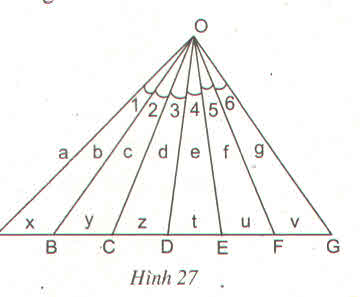
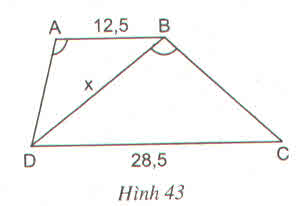
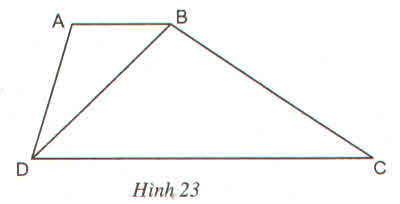
Xét ∆ABD và ∆BDC có:

=> ∆ABD ∽ ∆BDC(trường hợp 3)

=> BD = √(AB.DC) = √(12,5.8,5) = √356,25 => BD = 18,9 cm

A B C D E F H G L M N P
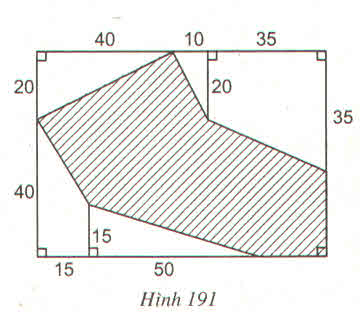
Độ dài chiều rộng của hình chữ nhật ABCD là:
20 + 40 = 60 (m)
Độ dài chiều dài của hình chữ nhật ABCD là:
40 + 10 + 35 = 85 (m)
Diện tích hình chữ nhật ABCD là:
60 . 85 = 5100 (m2).
Diện tích tam giác vuông HEN là:
\(\dfrac{10.20}{2}\)= \(\dfrac{200}{2}=100\left(m^2\right)\)
Diện tích tam giác vuông AHG là:
\(\dfrac{20.40}{2}=\dfrac{800}{2}=400\left(m^2\right)\)
Diện tích tam giác vuông MLP là:
\(\dfrac{15.50}{2}=\dfrac{750}{2}=375\left(m^2\right)\)
Diện tích hình thang vuông EBNF là:
\(\dfrac{\left(20+35\right).35}{2}=\dfrac{1925}{2}=962,5\left(m^2\right)\)
Diện tích hình thang vuông GMCL là:
\(\dfrac{\left(40+15\right).15}{2}=\dfrac{825}{2}=412,5\left(m^2\right)\)
Tổng diện tích các hình nằm ngoài hình gạch sọc và nằm trong hình chữ nhật ABCD là:
100 + 400 + 375 + 962,5 + 412,5 = 2250 (m2).
Diện tích hình sọc dọc là:
5100 - 2250 = 2850 (m2).
Vậy diện tích hình sọc dọc là 2850m2.

Ta có:
SABCD=(40+10+35).(20+40) = 5100 (cm2)
S1=\(\dfrac{40.20}{2}=400\left(cm^2\right)\)
S2=\(\dfrac{10.20}{2}=100\left(cm^2\right)\)
S3=\(\dfrac{\left(20+35\right).35}{2}=962,5\left(cm^2\right)\)
S4=\(\dfrac{50.15}{2}=375\left(cm^2\right)\)
S5=\(\dfrac{\left(15+40\right).15}{2}=412,5\left(cm^2\right)\)
=> Shình gạch sọc= S - ( S1+S2+S3+S4+S5)= 5100-(400+100+962,5+375+412,5)=2850(cm2)

Bài 1: Nhường chủ tus và các bạn:D
Bài 2(ko chắc nhưng vẫn làm:v): A B C D O
Do OA = OB(*) nên \(\Delta\)OAB cân tại O nên ^OAB = ^OBA (1)
Mặt khác cho AB // CD nên^OAB = ^OCD; ^OBA = ^ODC (so le trong) (2)
Từ (1) và (2) có ^OCD = ^ODC nên \(\Delta\) ODC cân tại O nên OC = OD (**)
Cộng theo vế (*) và (**) thu được:OA + OC = OB + OD
Hay AC = BD. Do đó hình thang ABCD có 2 đường chéo bằng nhau nên nó là hình thang cân (đpcm)



Giải
OB là tia phân giác trong của ∆OBC => xaxa = ycyc
OC là tia phân giác trong của ∆OBD => ydyd = zdzd
OD là tia phân giác trong của ∆OCE => zczc = tete
OE là tia phân giác trong của ∆ODF => tdtd = ufuf
OC là tia phân giác của ∆ACE => OCOAOCOA = CEOECEOE hay x+yax+ya = z+tez+te
OE là phân giác của ∆OCG => z