Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Giả sử \(\Delta ABC\)đều ngoại tiếp đường tròn (I), khi đó ta cần tính BC (hoặc AB, AC đều được)
Kẻ đường cao AH của \(\Delta ABC\). Nối B với I.
Ta ngay lập tức có BI là tia phân giác của \(\widehat{ABC}\)(vì I là tâm đường tròn nội tiếp \(\Delta ABC\))
Mà \(\widehat{ABC}=60^0\)(do \(\Delta ABC\)đều) \(\Rightarrow\widehat{IBH}=\frac{60^0}{2}=30^0\)
\(\Delta IBH\)vuông tại H \(\Rightarrow BH=IH.\cot\widehat{IBH}=r.\cot30^0=r\sqrt{3}\)
Mặt khác \(\Delta ABC\)đều có đường cao AH \(\Rightarrow\)AH cũng là trung tuyến \(\Rightarrow\)H là trung điểm BC
\(\Rightarrow BC=2BH=2r\sqrt{3}\)\(\Rightarrow\)Chọn ý thứ ba.
Tâm O của đường tròn nội tiếp tam giác đều cũng là giao điểm ba đường trung tuyến, ba đường cao.
Do đó đường cao h=AE=3.OE=3cm.
Trong tam giác đều, h = a√3/2 (a là độ dài mỗi cạnh).
Suy ra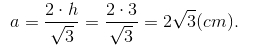 
Do đó diện tích tam giác ABC là
Ta chọn (D).
Gọi A; B; CD,E,F làn lượt là tiếp điểm của đường tròn nội tiếp tam giác với BC; CA; AB
Khi đó: \(S=S_{BIC}+S_{CAI}+S_{BAI}=\frac{1}{2}\) \(BC.ID+CA.IE+AB.IF=p.r\)
\(\frac{S}{h_a}+\frac{S}{h_b}+\frac{S}{h_c}=\frac{1}{2}\) \(a+b+c=p=\frac{S}{r}\)
\(\RightarrowĐPCM\)
Không tính tổng quát, giả sử: \(h_a\le h_b\le h_c\)
\(\Rightarrow\frac{1}{h_a}\ge\frac{1}{h_b}\ge\frac{1}{h_c}\)
\(\Rightarrow\frac{1}{h_a}\ge\frac{1}{3}\)
\(\Rightarrow h_a\le3\)
Mặt khác: \(\frac{1}{h_a}< \frac{1}{r}=1\Rightarrow h_a>1\Rightarrow h_a\ge2\)
Vậy: \(h_a=2\)hoặc \(h_a=3\)
Nếu \(h_a=2\)
\(\frac{1}{h_b}+\frac{1}{h_c}=1-\frac{1}{2}=\frac{1}{2}\)**
Ta có: \(a\ge b\ge c\)do \(h_a\le h_b\le h_c\)
Để a; b; clà 3 cạnh của một hình tam giác ta chỉ cần b + c > a do khi \(a\ge b\ge c\)theo ta sẽ có ngay a + c > b, a + b > c
\(\Leftrightarrow\frac{S}{h_b}+\frac{S}{h_c}>\frac{S}{h_a}\)
\(\Leftrightarrow\frac{1}{h_b}+\frac{1}{h_c}>\frac{1}{h_a}=\frac{1}{2}\)mâu thuẫn với **
Vậy, loại trường hợp này.
\(\Rightarrow h_a=3\Rightarrow h_b\ge h_c\ge3\)
\(\frac{1}{h_b}+\frac{1}{h_c}=1-\frac{1}{3}=\frac{2}{3}\)
\(\frac{1}{h_b}\ge\frac{1}{h_c}\)
Suy ra: \(\frac{1}{h_b}\ge\frac{1}{3}\Rightarrow h_b\le3\)
Mà: \(h_b\ge\frac{1}{3}\Rightarrow h_b\le3\)
Vậy: \(h_b=3\Rightarrow h_c=3\)
\(\RightarrowĐPCM\)
Nhận xét : A, B, C, D có vai trò bình đẳng nhau nên nếu O không thuộc miền trong ∆ICD, chẳng hạn O thuộc miền trong ∆IAD, khi đó dễ dàng thấy S(ICD) < S(IAD). Vậy chỉ xét trường hợp O thuộc miền trong ∆ICD.
Vẽ OH _|_ AC tại H; Vẽ OK _|_ BK tại K => IK = OH; IH = OK. Đặt IC = a > 0; ID = b > 0;
Ta có: CH = IC - IH <=> CH² = IC² + IH² - 2IC.IH <=> OC² - OH² = IC² + OK² - 2IC.OK <=> 2IC.OK = IC² - OC² + (OH² + OK²) = IC² - OC² + OI² <=> 2a.OK = a² - 5 + 1 = a² - 4 <=> 2OK = a - 4/a <=> 4OK² = a² + 16/a² - 8 (1)
Tương tự : 4OH² = b² + 16/b² - 8 (2)
(1) + (2) : a² + b² + 16(1/a² + 1/b²) - 16 = 4(OH² + OK²) = 4OI² = 4
<=> a² + b² + 16(1/a² + 1/b²) = 20
<=> ab + 16/ab ≤ 10 (vì 2ab ≤ a² + b² ; 2/ab ≤ 1/a² + 1/b²)
<=> S² - 5S + 4 ≤ 0 ( với S = ab/2 = S(ICD))
<=> (S - 5/2)² ≤ 9/4
<=> - 3/2 ≤ S - 5/2 ≤ 3/2
<=> 1 ≤ S ≤ 4
Vậy Max S = 4 khi a = b = 2√2; Min S = 1 khi a = b = √2
Nguồn: https://vn.answers.yahoo.com/question/index?qid=20150404221719AAVrhVe
Ta có : \(R=\frac{a}{2Sin\left(\frac{180}{n}\right)}\)
=> \(a=R.2Sin\left(\frac{180}{n}\right)=2.2Sin\left(\frac{180}{6}\right)=2\left(cm\right)\)