Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Số bội giác của ảnh: \(G_{\infty}=\dfrac{\delta.OC_C}{f_1.f_2}=\dfrac{16.20}{1.4}=80\)
b) * Xét TH quan sát ở điểm cực viễn: (nhắm chừng vô cực)
d2'= -OCv= - vô cùng
l= f1+f2+ $ =21 cm ($: là độ dài quang học nhá bạn)
=>1/f2= 1/d2+ 1/d2' ( vì d2'= - vô cùng)
=> f2=d2=4 cm
=>d1'= l-d2=21-4=17 cm
=>d1= (d1'*f1)/(d1'-f1)=1.0625 cm
Ta có k=-d1'/d1=-16 =>|k|=16
Ta có: k= A1'B1'/ AB=
=> A1'B1'= |k|AB
tan@= A1'B1'/f2 = |k|AB/f2 (@ là góc trong ảnh đó bạn, cái này áp dụng hệ thức lượng trong tam giác vuông)
=> AB= tan@*f2/ |k|
=>AB= (tan 2' * 4)/ 16=0.0001454 m
Đặt f1 và f2 lần lượt là tiêu cự của vật kính và thị kính của kính thiên văn.
Xét các biểu thức:
1. f1 + f2; 2. 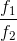 #Hỏi cộng đồng OLM
#Vật lý lớp 11
#Hỏi cộng đồng OLM
#Vật lý lớp 11


a) q = C. U = 1200µC = 1,2. 10 ¯ ³ C
b) Công của lực điện bằng độ biến thiên năng lượng điện trường của tụ
A = ΔWđ = W - W' = q²/2C - q'²/2C = (q-q')(q+q')/(2C) = Δq.(q + q - Δq)/2C ≈ 72.10 ¯ ⁶ J
c) Lúc điện tích tụ chỉ bằng q/2. Lập luận tương tự như trên, chỉ việc thay Δq = 0.001q = 1,2.10 ¯ ⁶ C
và q₁ = 0,6. 10 ¯ ³ C
Ta có:
A₁ = ΔWđ₁ = W₁ - W'₁ = q₁²/2C - q₁'²/2C = (q₁-q₁')(q₁+q₁')/(2C) = Δq.(q₁ + q₁ - Δq)/2C ≈ 36.10 ¯ ⁶ J
tại sao ở câu c bn lại có : \(\Delta q\)=1,2.10-6C và q1=0,6.10-3C ?

a)Điện tích của q : q =Cu = 12.10-4 C.
b) Vì lượng điện tích rất nhỏ, nên điện tích và đo đó cả hiệu điện thế giữa hai bản tụ coi như không thay đổi. Công của lực điện sinh ra sẽ là:
A = ∆q.U = 72.10-6 J.
c) Điện tích của tụ giảm một nửa thì hiệu điện thế giữa hai đầu bản tụ cũng giảm một nửa.
U'= U/2=30V
⇒ A’ = ∆q.U’ = 36.10-6 J.
Đáp án C
+ Độ bội giác của kính hiển vi khi ngắm chừng ở vô cực G ∞ = δ D f 1 f 2 .