
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(A=\left[\dfrac{\sqrt{x}-2}{x-1}-\dfrac{\sqrt{x}+2}{x+2\sqrt{x}+1}\right]\left[\dfrac{x^2-2x+1}{2}\right]\)
\(A=\left[\dfrac{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)^2}{\left(x-1\right)\left(\sqrt{x}+1\right)^2}-\dfrac{\left(\sqrt{x}+2\right)\left(x-1\right)}{\left(x-1\right)\left(\sqrt{x}+1\right)^2}\right]\) \(\left[\dfrac{\left(x-1\right)^2}{2}\right]\)
\(A=\left[\dfrac{\left(\sqrt{x}-2\right)\left(x+2\sqrt{x}+1\right)-\left(x\sqrt{x}-\sqrt{x}+2x-2\right)}{\left(x-1\right)\left(\sqrt{x}+1\right)^2}\right]\) \(\dfrac{\left(x-1\right)^2}{2}\)
\(A=\left[\dfrac{x\sqrt{x}+2x+\sqrt{x}-2x-4\sqrt{x}-2-x\sqrt{x}+\sqrt{x}-2x+2}{\left(x-1\right)\left(\sqrt{x}+1\right)^2}\right]\)
\(A=\dfrac{\left(x-1\right)\left(x-1\right)}{2}\)
\(A=\dfrac{-2x-2\sqrt{x}}{\left(x-1\right)\left(\sqrt{x}+1\right)^2}.\dfrac{\left(x-1\right)\left(x-1\right)}{2}\)
\(A=\dfrac{-2\sqrt{x}\left(\sqrt{x}+1\right)}{\left(\sqrt{x}+1\right)^2}.\dfrac{x-1}{2}\)
\(A=-\sqrt{x}\left(\sqrt{x}-1\right)\)


a) ta có : \(P=\left(\dfrac{\sqrt{x}-2}{x-1}-\dfrac{\sqrt{x}+2}{x+2\sqrt{x}+1}\right).\left(\dfrac{1-x}{\sqrt{2}}\right)^2\)
\(\Leftrightarrow P=\left(\dfrac{\sqrt{x}-2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}-\dfrac{\sqrt{x}+2}{\left(\sqrt{x}+1\right)^2}\right).\left(\dfrac{1-x}{\sqrt{2}}\right)^2\)
\(\Leftrightarrow P=\left(\dfrac{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)-\left(\sqrt{x}+2\right)\left(\sqrt{x}-1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)^2}\right).\left(\dfrac{1-x}{\sqrt{2}}\right)^2\)
\(\Leftrightarrow P=\left(\dfrac{-2\sqrt{x}}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)^2}\right).\left(\dfrac{1-x}{\sqrt{2}}\right)^2\) \(\Leftrightarrow P=\left(\dfrac{-2\sqrt{x}}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)^2}\right).\dfrac{\left(\sqrt{x}-1\right)^2\left(\sqrt{x}+1\right)^2}{2}\) \(\Leftrightarrow P=\sqrt{x}-x\)b) ta có : \(x< 1\Leftrightarrow x-1< 0\Leftrightarrow\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)< 0\)
\(\Leftrightarrow\sqrt{x}-1< 0\Leftrightarrow x-\sqrt{x}< 0\Leftrightarrow\sqrt{x}-x>0\)
\(\Leftrightarrow P>0\left(đpcm\right)\)

\(\left(\frac{\sqrt{x}-2}{x-1}-\frac{\sqrt{x}+2}{x+2\sqrt{x}+1}\right).\frac{x^2-2x+1}{2}\)
a)
Đkxđ:\(\left\{{}\begin{matrix}x-1\ne0\\x\ge0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\ne1\\x\ge0\end{matrix}\right.\)
\(=\)\(\left(\frac{\sqrt{x}-2}{x-1}-\frac{\sqrt{x}+2}{x+2\sqrt{x}+1}\right).\frac{\left(x-1\right)^2}{2}\)
\(=\frac{x\sqrt{x}+2x+\sqrt{x}-2x-4\sqrt{x}-2-x\sqrt{x}+\sqrt{x}-2x+2}{\left(x-1\right)\left(x+2\sqrt{x}+1\right)}.\frac{\left(x-1\right)^2}{2}\)
\(=\frac{-2\sqrt{x}-2x}{\left(x-1\right)\left(\sqrt{x}+1\right)^2}.\frac{\left(x-1\right)^2}{2}\)
\(=\frac{-2\sqrt{x}\left(1+\sqrt{x}\right)}{\left(x-1\right)\left(\sqrt{x}+1\right)^2}.\frac{\left(x-1\right)^2}{2}\)
\(=\frac{-2\sqrt{x}\left(x-1\right)}{2\left(\sqrt{x}+1\right)}=\frac{-2\sqrt{x}\left(x-1\right)}{2\sqrt{x}+2}\)

mình giải thế này
a)\(P=\left(\frac{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)^2}-\frac{\left(\sqrt{x}+2\right)\left(\sqrt{x}-1\right)}{\left(\sqrt{x}+1\right)^2\left(\sqrt{x}-1\right)}\right)\frac{\left(1-x\right)^2}{2}\)
\(P=\frac{-2\sqrt{x}}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)^2}.\frac{\left(\sqrt{x}-1\right)^2\left(\sqrt{x+1}\right)^2}{2}\)
\(P=-\sqrt{x}.\left(\sqrt{x}-1\right)=-x+\sqrt{x}\)
b)\(0< x< 1\Rightarrow\sqrt{x}< 1\Rightarrow\sqrt{x}-1< 0\)
\(\Rightarrow-x\left(\sqrt{x}-1\right)>0\)vì \(x>0\)
xong rồi nhé :)

Lời giải:
Áp dụng định lý Vi-et: \(\left\{\begin{matrix} x_1+x_2=-10\\ x_1x_2=-2018\end{matrix}\right.\)
Do đó:
\((x_1-10)(x_2-10)=x_1x_2-10(x_1+x_2)+100\)
\(=-2018-10(-10)+100=-2018< 0\)
\(\Rightarrow x_1< 10< x_2\) nếu $x_1< x_2$ (đpcm)
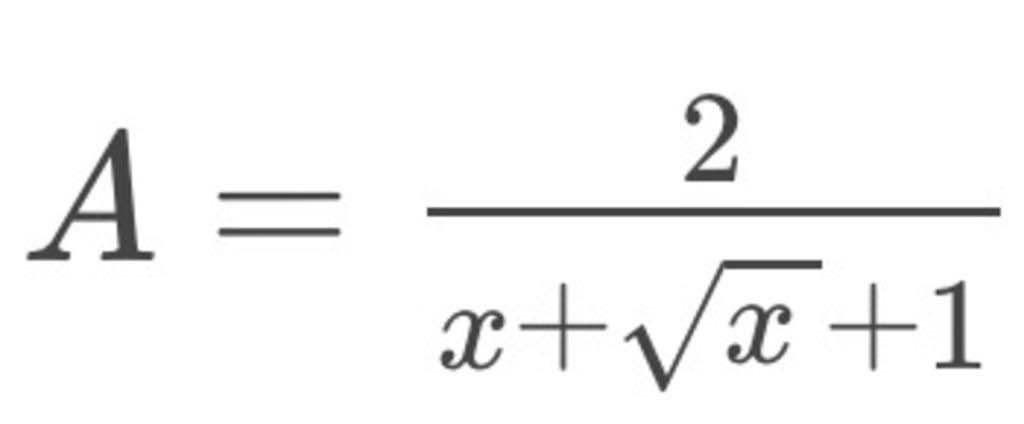 ĐK: x≥0, x khác 1
ĐK: x≥0, x khác 1