
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



\(\int\limits^1_0x^3e^{x^2}dx=\int\limits^1_0x^3e^{x^2}.xdx\)
Đặt \(t=x^2\Rightarrow\begin{cases}dt=2xdx;x=0\rightarrow t=0,x=1\rightarrow t=1\\f\left(x\right)dx=te^tdt\end{cases}\)
Do đó : \(I=\int\limits^1_0te^1dt=\frac{1}{2}\int\limits^1_0t.d\left(e^t\right)=\frac{1}{2}\left(t.e^t-e^t\right)|^1_0=\frac{1}{2}\)

\(\int\limits^{\frac{\pi}{2}}_0x.\sin^2xdx=\int\limits^{\frac{\pi}{2}}_0x\left(\frac{1-\cos2x}{2}\right)dx=\frac{1}{2}\left[\int\limits^{\frac{\pi}{2}}_0xdx-\int\limits^{\frac{\pi}{2}}_0x.\cos3xdx\right]\)
\(=\frac{1}{2}\left(\frac{1}{2}x^2|^{\frac{\pi}{2}}_0-\frac{1}{2}\int\limits^{\frac{\pi}{2}}_0x.d\left(\sin2x\right)\right)\)
\(=\frac{1}{2}\left[\frac{\pi^2}{8}-\frac{1}{2}\left(x.\sin2x\right)|^{\frac{\pi}{2}}_0-\int\limits^{\frac{\pi}{2}}_0\sin2xdx\right]\)
\(=\frac{1}{2}\left[\frac{\pi^2}{8}-\frac{1}{2}\left(0+\frac{1}{2}\cos2x|^{\frac{\pi}{2}}_0\right)\right]=\frac{\pi^2+8}{16}\)

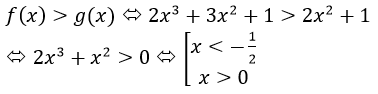
dùng symbolab à?
Mình được một người bạn nhờ vả, mà làm sao để tìm được "undefined points" ???? , mình đa phần sẽ giải Lim nhưng sẽ giải như thế nào ở bài này để tìm nó ?