MC
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
CM
20 tháng 12 2019
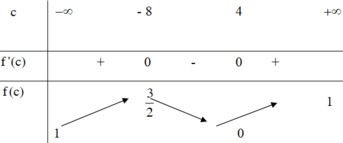
Đáp án D
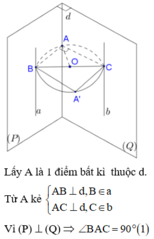
Ta đi chứng minh BC chính là khoảng cách giữa hai đường thẳng a và b, BC = 4:
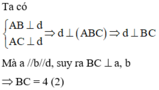
Từ (1) (2) suy ra A thuộc đường tròn đường kính BC bằng 4 không đổi
Do đó d thuộc mặt trụ có khoảng cách giữa đường sinh và trục bằng 2
1 tháng 4 2016
Xét đường thẳng ∆ đi qua điểm O và vuông gó với mặt phẳng (P). Gọi l là đưởng thẳng đi qua M0 ε (C) và l vuông góc với (P). Do đó l // ∆. Quay mặt phẳng (Q) tạo bởi l và ∆ quanh đường thẳng ∆, thì đường thẳng l vạch lên một mặt trụ tròn xoay. Mặt trụ này chứa tất cả những đường thẳng đi qua các điểm M ε (C) và vuông góc với (P). Trục của mặt trụ là ∆ và bán kính của trụ bằng r.
CM
13 tháng 10 2019
Chọn A.
Phương pháp:
Góc giữa đường thẳng d và mặt phẳng (P) là góc giữa đường thẳng d và đường thẳng d’ là hình chiếu của d trên (P).
Cách giải:
Suy ra hình chiếu của SB lên (ABC) là AB.
Do đó, góc giữa SB và (ABC) là góc giữa SB và AB.
CM
18 tháng 4 2017
Đáp án A
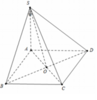
Ta có C B ⊥ A B C B ⊥ S A ⇒ C B ⊥ ( S A B )
Do đó S C ; S A B ^ = C S B ^ = α
⇒ S B = a tan α = 5 a 10 ⇒ S A = S B 2 - A B 2 = a 6 2
Ta có S O ; A B C D ^ = S O A ^ trong đó t a n S C A ^ = S A O A = a 6 2 a 2 2 = 3 .
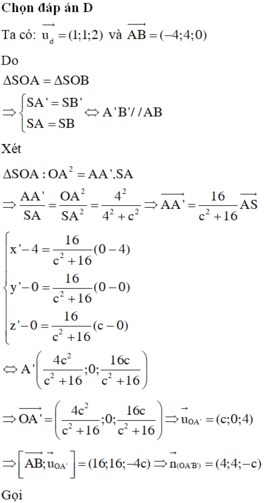
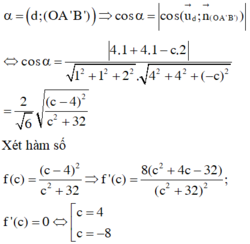
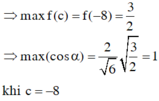
Định lý 1: Trong các đường xiên và đường vuông góc kẻ từ một điểm ở ngoài một đường thẳng đến đường thẳng đó, đường vuông góc là đường ngắn nhất.
Định lý 2: Trong hai đường xiên kẻ từ một điểm nằm ngoài một đường thẳng đến đường thẳng đó;
a) Đường xiên nào có hình chiếu lớn hơn thì lớn hơn
b) Đường xiên nào lớn hơn thì có hình chiếu lớn hơn
c) Nếu hai đường xiên bằng nhau thì hai hình chiếu bằng nhau và ngược lại nếu hai hình chiếu bằng nhau thì hai đường xiên bằng nhau.