Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

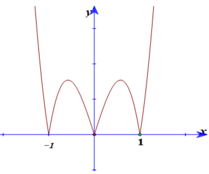
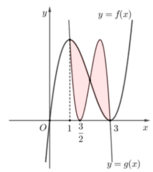
+ Từ đồ thị của hàm số và a> 0 ta dễ dàng có được đồ thị hàm số y= f’(x) như sau:
Ta có : f’(x) = 4ax3+ 2bx
Đồ thị hàm số y= f’(x) đi qua 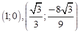 ta tìm được a=1 và b= -2
ta tìm được a=1 và b= -2
Suy ra hàm số đã cho có dạng: f(x) =x4-2x2+d và f’(x) = 4x3-4x.
+ Do (C) tiếp xúc với trục hoành nên f’(x) = 0 khi x=0; x=1; x=- 1.
Do (C) đối xứng qua trục tung nên (C) tiếp xúc với trục hoành tại 2 điểm (1; 0) và (-1; 0).
Do đó: f(0) =1 suy ra 1= 0-2.0+ d nên d= 1
Vậy hàm số cần tìm là: y =x4-2x2+1
+ Xét phương trình hoành độ giao điểm của (C) với trục hoành:
x4-2x2+1 =0 nên x=± 1
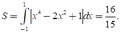
Chọn D.

Đáp án A
Phương pháp:
Phương trình a n x n + a n - 1 x n - 1 + . . . + a 1 x + a 0 = 0 có n nghiệm phân biệt x1, x2, ...,xn được viết dưới dạng a n x - x 1 x - x 2 . . . x - x n = 0
Cách giải:
Gọi phương trình đường thẳng d:
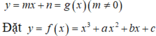
Xét phương trình hoàng độ giao điểm
f(x) - g(x) = 0
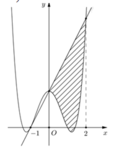
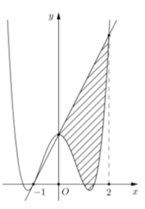
Đường thẳng d cắt (C) tại điểm A có hoành độ -1 và điểm B có hoành độ bằng 2 .
![]()
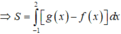
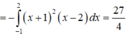



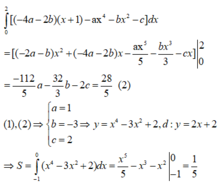
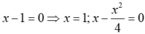
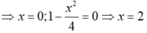

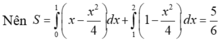


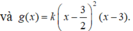 .
.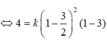 .
.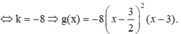
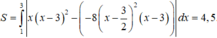
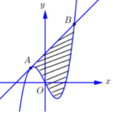
Lời giải:
Sử dụng công thức phương trình tiếp tuyến tại \(x_0\) là:
\(y=f'(x_0)(x-x_0)+f(x_0)\)
Ta có phương trình hai đường thẳng là tiếp tuyến của đồ thị \(y=x^2-4x+5\) tại \(A,B\) là:\(\left\{\begin{matrix}y=-2x+4\\y=4x-11\end{matrix}\right.\)
Ta có: \(x^2-4x+5-(-2x+4)=x^2-2x+1=(x-1)^2=0\Leftrightarrow x=1\)
\(x^2-4x+5-(4x-11)=(x-4)^2=0\Leftrightarrow x=4\)
\((-2x+4)-(4x-11)=0\Leftrightarrow x=\frac{5}{2}\)
Do đó diện tích hình phẳng giới hạn bởi các đường đã cho là:
\(\int ^{4}_{\frac{5}{2}}|(x-4)^2|dx+\int ^{\frac{5}{2}}_{1}|(x-1)^2|dx=\frac{9}{8}+\frac{9}{8}=\frac{9}{4}\)
\(\Rightarrow a+b=9+4=13\)
cảm ơn nha