Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Câu 1:
\(AB=\sqrt{\left[3-\left(-2\right)\right]^2+\left(3-2\right)^2}=\sqrt{26}\)
\(BC=\sqrt{\left(2-3\right)^2+\left(-2-3\right)^2}=\sqrt{26}\)
\(AC=\sqrt{\left[2-\left(-2\right)\right]^2+\left(-2-2\right)^2}=4\sqrt{2}\)
\(P=\dfrac{AB+BC+AC}{2}=\dfrac{2\sqrt{26}+4\sqrt{2}}{2}=\sqrt{26}+2\sqrt{2}\)
\(S=\sqrt{\left(\sqrt{26}+2\sqrt{2}\right)\cdot2\sqrt{2}\cdot2\sqrt{2}\cdot\left(\sqrt{26}-2\sqrt{2}\right)}=\sqrt{18\cdot8}=12\left(đvdt\right)\)

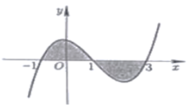
Phương trình hoành độ giao điểm của đồ thị hàm số y=f(x) và trục hoành:
1 3 x 3 - x 2 - 1 3 x + 1 = 0 ⇔ [ x = 1 x = - 1 x = 3
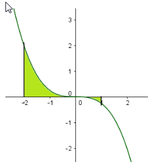
Từ hình vẽ ta thấy f ( x ) > 0 , ∀ x ∈ - 1 ; 1
và f ( x ) < 0 , ∀ x ∈ ( 1 ; 3 )
Do đó 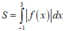
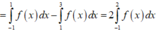
Suy ra các phương án A, C, D đúng.
Chọn đáp án B.
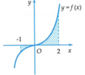
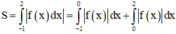

Đáp án C
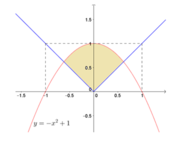
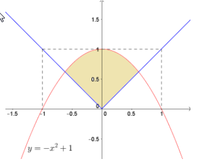
Đây là diện tích hình phẳng được giới hạn bởi đồ thị hàm số y = |x| và y = - x 2 + 1
Phương trình hoành độ giao điểm:
Diện tích hình phẳng cần tính là S = ∫ 1 - 5 2 0 - x 2 + 1 + x d x + ∫ 0 - 1 + 5 2 - x 2 + 1 - x d x