Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

b: \(\Leftrightarrow\dfrac{7x+10}{x+1}\left(x^2-x-2-2x^2+3x+5\right)=0\)
\(\Leftrightarrow\left(7x+10\right)\left(-x^2+2x+3\right)=0\)
\(\Leftrightarrow\left(7x+10\right)\left(x^2-2x-3\right)=0\)
=>(7x+10)(x-3)=0
hay \(x\in\left\{-\dfrac{10}{7};3\right\}\)
d: \(\Leftrightarrow\dfrac{13}{2x^2+7x-6x-21}+\dfrac{1}{2x+7}-\dfrac{6}{\left(x-3\right)\left(x+3\right)}=0\)
\(\Leftrightarrow\dfrac{13}{\left(2x+7\right)\left(x-3\right)}+\dfrac{1}{\left(2x+7\right)}-\dfrac{6}{\left(x-3\right)\left(x+3\right)}=0\)
\(\Leftrightarrow26x+91+x^2-9-12x-14=0\)
\(\Leftrightarrow x^2+14x+68=0\)
hay \(x\in\varnothing\)

\(1.\text{ }\text{ }\text{ }\dfrac{\left(x^2+2\right)^2-4x^2}{y\left(x^2+2\right)-2xy-\left(x-1\right)^2-1}\\ =\dfrac{\left(x^2+2-2x\right)\left(x^2+2+2x\right)}{x^2y+2y-2xy-x^2+2x-1-1}\\ =\dfrac{\left(x^2+2-2x\right)\left(x^2+2+2x\right)}{\left(x^2y-x^2\right)-\left(2xy-2x\right)+\left(2y-2\right)}\\ =\dfrac{\left(x^2+2-2x\right)\left(x^2+2+2x\right)}{x^2\left(y-1\right)-2x\left(y-1\right)+2\left(y-1\right)}\\ =\dfrac{\left(x^2+2-2x\right)\left(x^2+2+2x\right)}{\left(x^2-2x+2\right)\left(y-1\right)}\\ =\dfrac{x^2+2x+2}{y-1}\)
\(2.\text{ }\text{ }\text{ }\text{ }\dfrac{x^2+5x+6}{x^2+3x+2}\\ =\dfrac{x^2+3x+2x+6}{x^2+2x+x+2}\\ =\dfrac{\left(x^2+3x\right)+\left(2x+6\right)}{\left(x^2+2x\right)+\left(x+2\right)}\\ =\dfrac{x\left(x+3\right)+2\left(x+3\right)}{x\left(x+2\right)+\left(x+2\right)}\\ =\dfrac{\left(x+2\right)\left(x+3\right)}{\left(x+2\right)\left(x+1\right)}\\ =\dfrac{x+3}{x+1}\)
\(3.\text{ }\text{ }\text{ }\dfrac{x^2+y^2-z^2-2zt+2xy-t^2}{x^2-y^2+z^2-2yt+2xz-t^2}\text{ ( Chữa đề ) }\\ =\dfrac{\left(x^2+2xy+y^2\right)-\left(z^2+2zt+t^2\right)}{\left(x^2+2xz+z^2\right)-\left(y^2+2yt+t^2\right)}\\ =\dfrac{\left(x+y\right)^2-\left(z+t\right)^2}{\left(x+z\right)^2-\left(y+t\right)^2}\\ =\dfrac{\left(x+y+z+t\right)\left(x+y-z-t\right)}{\left(x+z+y+t\right)\left(x+z-y-t\right)}\\ =\dfrac{x+y-z-t}{x+z-y-t}\)
\(4.\text{ }\text{ }\text{ }\dfrac{\left(n+1\right)!}{\left(n+1\right)!+\left(n+2\right)!}=\dfrac{\left(n+1\right)!}{\left(n+1\right)!\left(1+n+2\right)}=\dfrac{1}{n+3}\)
\(5.\text{ }\text{ }\text{ }\dfrac{x^2+5x+4}{x^2-1}\\ =\dfrac{x^2+x+4x+4}{\left(x+1\right)\left(x-1\right)}\\ =\dfrac{\left(x^2+x\right)+\left(4x+4\right)}{\left(x+1\right)\left(x-1\right)}\\ =\dfrac{x\left(x+1\right)+4\left(x+1\right)}{\left(x+1\right)\left(x-1\right)}\\ =\dfrac{\left(x+1\right)\left(x+4\right)}{\left(x+1\right)\left(x-1\right)}\\ =\dfrac{x+4}{x-1}\)
\(6.\text{ }\text{ }\text{ }\dfrac{x^2-3x}{2x^2-7x+3}\\ =\dfrac{x\left(x-3\right)}{2x^2-6x-x+3}\\ =\dfrac{x\left(x-3\right)}{\left(2x^2-6x\right)-\left(x-3\right)}\\ =\dfrac{x\left(x-3\right)}{2x\left(x-3\right)-\left(x-3\right)}\\ =\dfrac{x\left(x-3\right)}{\left(2x-1\right)\left(x-3\right)}\\ =\dfrac{x}{2x-1}\)

1) \(\dfrac{A\left(x-5\right)}{\left(x+1\right)\left(x-5\right)}=\dfrac{3x\left(x+3\right)}{\left(x+1\right)\left(x+3\right)}\)
\(\Rightarrow A=3x\)
2) \(\dfrac{\left(x+3\right)\left(x-2\right)}{A\left(x-3\right)}=\dfrac{\left(5x-1\right)\left(x-2\right)}{\left(5x-1\right)\left(x^2+3\right)}\)
\(\Leftrightarrow\dfrac{\left(x+3\right)}{A\left(x-3\right)}=\dfrac{1}{\left(x^2+3\right)}\)
\(\Rightarrow A=\dfrac{\left(x^2+3\right)\left(x+3\right)}{x-3}\)
3) \(\dfrac{\left(x-5\right)\left(x+5\right)}{\left(x+5\right)\left(2x-3\right)}=\dfrac{\left(x-5\right)A}{\left(2x-3\right)\left(x+2\right)}\)
\(\Leftrightarrow1=\dfrac{A}{\left(x+2\right)}\)
\(\Leftrightarrow A=x+2\)

Bài 1:
a) \(\dfrac{3x^2-5}{x^2-5x}+\dfrac{5-15x}{5x-25}\)
\(=\dfrac{3x^2-5}{x\left(x-5\right)}+\dfrac{5\left(1-3x\right)}{5\left(x-5\right)}\)
\(=\dfrac{3x^2-5}{x\left(x-5\right)}+\dfrac{1-3x}{x-5}\)
\(=\dfrac{3x^2-5}{x\left(x-5\right)}+\dfrac{x\left(1-3x\right)}{x\left(x-5\right)}\)
\(=\dfrac{3x^2-5+x\left(1-3x\right)}{x\left(x-5\right)}\)
\(=\dfrac{3x^2-5+x-3x^2}{x\left(x-5\right)}\)
\(=\dfrac{-5+x}{x\left(x-5\right)}\)
\(=\dfrac{x-5}{x\left(x-5\right)}\)
\(=\dfrac{1}{x}\)
b) \(\dfrac{4+x^3}{x-3}-\dfrac{2x+2x^2}{x-3}+\dfrac{2x-13}{x-3}\)
\(=\dfrac{\left(4+x^3\right)-\left(2x+2x^2\right)+\left(2x-13\right)}{x-3}\)
\(=\dfrac{4+x^3-2x-2x^2+2x-13}{x-3}\)
\(=\dfrac{x^3-2x^2-9}{x-3}\)
\(=\dfrac{x^3-3x^2+x^2-9}{x-3}\)
\(=\dfrac{x^2\left(x-3\right)+\left(x-3\right)\left(x+3\right)}{x-3}\)
\(=\dfrac{\left(x-3\right)\left(x^2+x+3\right)}{x-3}\)
\(=x^2+x+3\)
c) \(\dfrac{2}{x-5}+\dfrac{x-25}{\left(x+5\right)\left(x-5\right)}\)
\(=\dfrac{2\left(x+5\right)}{\left(x+5\right)\left(x-5\right)}+\dfrac{x-25}{\left(x+5\right)\left(x-5\right)}\)
\(=\dfrac{2\left(x+5\right)+x-25}{\left(x+5\right)\left(x-5\right)}\)
\(=\dfrac{2x+10+x-25}{\left(x+5\right)\left(x-5\right)}\)
\(=\dfrac{3x-15}{\left(x+5\right)\left(x-5\right)}\)
\(=\dfrac{3\left(x-5\right)}{\left(x+5\right)\left(x-5\right)}\)
\(=\dfrac{3}{x+5}\)
d) Đề sai?
Bài 2:
\(A=2\left(x+1\right)+\left(3x+2\right)\left(3x-2\right)-9x^2\)
\(A=2x+2+9x^2-4-9x^2\)
\(A=2x-2\)
\(A=2\left(x-1\right)\)
Thay x = 15 vào A ta được:
\(A=2\left(15-1\right)\)
\(A=2.14=28\)

Giải:
a) \(8\left(3x-2\right)-13x=5\left(12-3x\right)+7x\)
\(\Leftrightarrow24x-16-13x=60-15x+7x\)
\(\Leftrightarrow24x-13x+15x-7x=60+16\)
\(\Leftrightarrow19x=76\)
\(\Leftrightarrow x=\dfrac{76}{19}=4\)
Vậy ...
b) \(\dfrac{5x}{x+2}-\dfrac{3}{x-2}+\dfrac{3x^2+6}{\left(x-2\right)\left(x+2\right)}=0\) (1)
ĐKXĐ: \(x\ne\pm2\)
\(\left(1\right)\Leftrightarrow\dfrac{5x\left(x-2\right)}{\left(x-2\right)\left(x+2\right)}-\dfrac{3\left(x+2\right)}{\left(x-2\right)\left(x+2\right)}+\dfrac{3x^2+6}{\left(x-2\right)\left(x+2\right)}=0\)
\(\Leftrightarrow5x\left(x-2\right)-3\left(x+2\right)+3x^2+6=0\)
\(\Leftrightarrow5x^2-10x-3x-6+3x^2+6=0\)
\(\Leftrightarrow8x^2-13x=0\)
\(\Leftrightarrow x\left(8x-13\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\8x-13=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\left(TM\right)\\x=\dfrac{13}{8}\left(TM\right)\end{matrix}\right.\)
Vậy ...
c) \(\dfrac{x}{2\left(x-3\right)}+\dfrac{x}{2x+2}=\dfrac{2x}{\left(x+1\right)\left(x-3\right)}\) (2)
ĐKXĐ: \(x\ne-1;x\ne3\)
\(\left(2\right)\Leftrightarrow\dfrac{x\left(x+1\right)}{2\left(x-3\right)\left(x+1\right)}+\dfrac{x\left(x-3\right)}{2\left(x+1\right)\left(x-3\right)}=\dfrac{4x}{2\left(x+1\right)\left(x-3\right)}\)
\(\Leftrightarrow x\left(x+1\right)+x\left(x-3\right)=4x\)
\(\Leftrightarrow x\left(x+1+x-3\right)=4x\)
\(\Leftrightarrow x\left(2x-2\right)=4x\)
\(\Leftrightarrow2x-2=4\)
\(\Leftrightarrow x=3\)
Vậy ...

Hướng dẫn thôi nha bạn.
Giải:
Bài 1.
- Nhân đơn thức với đa thức: Nhân đơn thức với từng hạng tử của đa thức. (Rút gọn các hạng tử đồng dạng)
VD: Câu a)
\(2x\left(x^2-7x-3\right)\)
\(=2x.x^2-2x.7x-2x.3\)
\(=2x^3-14x^2-6x\)
- Nhân đa thức với đa thức: Nhân từng hạng tử của đa thức này với từng hạng tử của đa thức kia. (Rút gọn các hạng tử đồng dạng)
VD: Câu e)
\(\left(x^2-2x+3\right)\left(x-4\right)\)
\(=x^2.x-x^2.4-2x.x+2x.4+3.x-3.4\)
\(=x^3-4x^2-2x^2+8x+3x-12\)
\(=x^3-6x^2+11x-12\)
Bài 2.
Áp dụng hằng đẳng thức (số 1 và số 2)
VD: \(892^2+892.216+108^2\)
\(=892^2+2.892.108+108^2\)
\(=\left(892+108\right)^2\)
\(=1000^2=1000000\)
Bài 3: Chủ yếu áp dụng hằng đẳng thức và phương pháp đặt nhân tử.
VD: Câu a)
\(7x^2-28=0\)
\(\Leftrightarrow7\left(x^2-4\right)=0\)
\(\Leftrightarrow x^2-4=0\left(7\ne0\right)\)
\(\Leftrightarrow\left(x-2\right)\left(x+2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x+2=0\\x-2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-2\\x=2\end{matrix}\right.\)
Bài 4: Áp dụng hằng đẳng thức
\(M=\left(x+3\right)\left(x^2-3x+9\right)-\left(x^3+54-x\right)\)
\(\Leftrightarrow M=x^3+27-\left(x^3+54-x\right)\)
\(\Leftrightarrow M=x^3+27-x^3-54+x\)
\(\Leftrightarrow M=-27+x\)
Thay \(x=27\)
\(\Leftrightarrow M=-27+27=0\)
Vậy ...
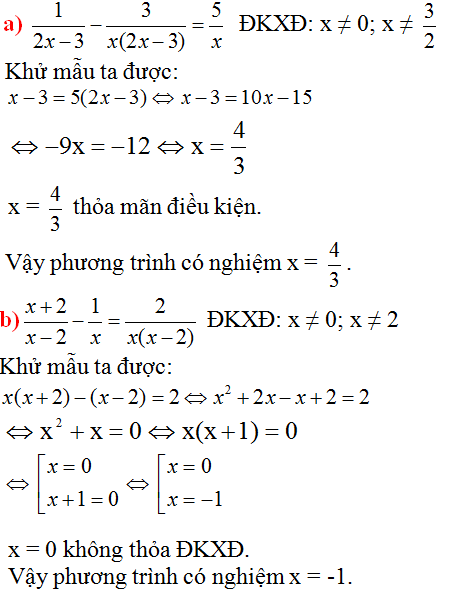


a, \(\dfrac{t+3}{t-2}+\dfrac{t-2}{t+3}=\dfrac{5t+15}{t^2+t-6}\) ĐKXĐ: t\(\ne\)2,t\(\ne\)-3
\(\Leftrightarrow\dfrac{t+3}{t-2}+\dfrac{t-2}{t+3}=\dfrac{5t+15}{\left(t+3\right)\left(t-2\right)}\)
\(\Rightarrow\left(t+3\right)\left(t+3\right)+\left(t-2\right)\left(t-2\right)=5t+15\)
\(\Leftrightarrow t^2+6t+9+t^2-4t+4-5t-15=0\)
\(\Leftrightarrow-3t-2=0\)
\(\Leftrightarrow-3t=2\)
\(\Leftrightarrow t=\dfrac{-2}{3}\) (tđk)
\(\Rightarrow S=\left\{\dfrac{-2}{3}\right\}\)
b, \(\left(2x+3\right)\left(\dfrac{3x+8}{2-7x}+1\right)=\left(x-5\right)\left(\dfrac{3x+8}{2-7x}+1\right)\)ĐKXĐ: x\(\ne\)\(\dfrac{2}{7}\)
\(\Leftrightarrow\) \(\left(2x+3\right)\left(\dfrac{3x+8}{2-7x}+1\right)-\left(x-5\right)\left(\dfrac{3x+8}{2-7x}+1\right)=0\)
\(\Rightarrow\left(\dfrac{3x+8}{2-7x}+1\right)\left(2x+3-x+5\right)=0\)
\(\Leftrightarrow\) \(\Rightarrow\left(\dfrac{3x+8}{2-7x}+1\right)\left(x+8\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}\dfrac{3x+8}{2-7x}+1=0\\x+8=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}3x+8+2-7x=0\\x=-8\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}-4x+10=0\\x=-8\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{5}{2}\\x=-8\end{matrix}\right.\)
\(\Rightarrow S=\left\{\dfrac{5}{2};-8\right\}\)
ĐKXĐ: x khác 2 và x khác -3
\(\dfrac{t+3}{t-2}+\dfrac{t-2}{t+3}=\dfrac{5t+15}{t^2+t-6}\)
\(\Leftrightarrow\dfrac{\left(t+3\right)\left(t+3\right)}{\left(t+3\right)\left(t-2\right)}+\dfrac{\left(t-2\right)\left(t-2\right)}{\left(t+3\right)\left(t-2\right)}=\dfrac{5t+15}{t^2+t-6}\)
\(\Rightarrow t^2+6t+9+t^2-4=5t+15\)
\(\Leftrightarrow2t^2+t-10=0\)
\(\Leftrightarrow2t^2-4t+5t-10=0\)
\(\Leftrightarrow2t\left(t-2\right)+5\left(t-2\right)=0\)
\(\Leftrightarrow\left(2t+5\right)\left(t-2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}t=2\left(loại\right)\\t=\dfrac{-5}{2}\end{matrix}\right.\)
Vậy..................