Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) \(\dfrac{4x-1}{3x^2y}-\dfrac{7x-1}{3x^2y}\)
\(=\dfrac{\left(4x-1\right)-\left(7x-1\right)}{3x^2y}\)
\(=\dfrac{4x-1-7x+1}{3x^2y}\)
\(=\dfrac{-3x}{3x^2y}\)
\(=\dfrac{-1}{xy}\)
b) \(\dfrac{4x+5}{2x-1}-\dfrac{5-9x}{2x-1}\)
\(=\dfrac{\left(4x+5\right)-\left(5-9x\right)}{2x-1}\)
\(=\dfrac{4x+5-5+9x}{2x-1}\)
\(=\dfrac{13x}{2x-1}\)
c) \(\dfrac{11x}{2x-3}-\dfrac{x-18}{3-2x}\)
\(=\dfrac{11x}{2x-3}+\dfrac{x-18}{2x-3}\)
\(=\dfrac{11x+\left(x-18\right)}{2x-3}\)
\(=\dfrac{11x+x-18}{2x-3}\)
\(=\dfrac{12x-18}{2x-3}\)
\(=\dfrac{6\left(2x-3\right)}{2x-3}\)
\(=\dfrac{6}{1}\)
\(=6\)
d) \(\dfrac{2x-7}{10x-4}-\dfrac{3x+5}{4-10x}\)
\(=\dfrac{2x-7}{10x-4}+\dfrac{3x+5}{10x-4}\)
\(=\dfrac{\left(2x-7\right)+\left(3x+5\right)}{10x-4}\)
\(=\dfrac{2x-7+3x+5}{10x-4}\)
\(=\dfrac{5x-2}{10x-4}\)
\(=\dfrac{5x-2}{2\left(5x-2\right)}\)
\(=\dfrac{1}{2}\)

a: \(=\dfrac{1}{x+2y}+\dfrac{1}{x-2y}-\dfrac{4y}{\left(x-2y\right)\left(x+2y\right)}\)
\(=\dfrac{x-2y+x+2y-4y}{\left(x+2y\right)\left(x-2y\right)}=\dfrac{2\left(x-2y\right)}{\left(x+2y\right)\left(x-2y\right)}=\dfrac{2}{x+2y}\)
b: \(=\dfrac{2x}{x-1}+\dfrac{5\left(x-1\right)\left(x+1\right)}{\left(x+1\right)^2}\cdot\dfrac{2\left(x+1\right)}{5\left(1-x\right)}\)
\(=\dfrac{2x}{x-1}-2=\dfrac{2x-2x+2}{x-1}=\dfrac{2}{x-1}\)
c: \(=\dfrac{5\left(x-1\right)}{2x}\cdot\dfrac{x^2+2x+1-x^2+2x-1}{\left(x-1\right)\left(x+1\right)}\)
\(=\dfrac{5\cdot4x}{2x\cdot\left(x+1\right)}=\dfrac{10}{x+1}\)

b: \(\Leftrightarrow\dfrac{2}{\left(x+7\right)\left(x-3\right)}=\dfrac{3x+21}{\left(x-3\right)\left(x+7\right)}\)
=>3x+21=2
=>x=-19/3
d: \(\Leftrightarrow\left(2x+1\right)^2-\left(2x-1\right)^2=8\)
\(\Leftrightarrow4x^2+4x+1-4x^2+4x-1=8\)
=>8x=8
hay x=1

Bài 2 .
a) \(\dfrac{2x}{x^2+2xy}+\dfrac{y}{xy-2y^2}+\dfrac{4}{x^2-4y^2}\)
\(=\dfrac{2x}{x\left(x+2y\right)}+\dfrac{y}{y\left(x-2y\right)}+\dfrac{4}{\left(x-2y\right)\left(x+2y\right)}\)
\(=\dfrac{2xy\left(x-2y\right)+xy\left(x+2y\right)+4xy}{xy\left(x+2y\right)\left(x-2y\right)}\)
\(=\dfrac{2x^2y-2xy^2+x^2y+2xy^2+4xy}{xy\left(x+2y\right)\left(x-2y\right)}\)
\(=\dfrac{3x^2y+4xy}{xy\left(x+2y\right)\left(x-2y\right)}\)
b) Sai đề hay sao ý
c) \(\dfrac{2x+y}{2x^2-xy}+\dfrac{16x}{y^2-4x^2}+\dfrac{2x-y}{2x^2+xy}\)
\(=\dfrac{2x+y}{x\left(2x-y\right)}+\dfrac{-16x}{\left(2x-y\right)\left(2x+y\right)}+\dfrac{2x-y}{x\left(2x+y\right)}\)
\(=\dfrac{\left(2x+y\right)^2-16x^2+\left(2x-y\right)^2}{x\left(2x-y\right)\left(2x+y\right)}\)
\(=\dfrac{4x^2+4xy+y^2-16x^2+4x^2-4xy+y^2}{x\left(2x-y\right)\left(2x+y\right)}\)
\(=\dfrac{-8x^2}{x\left(2x-y\right)\left(2x+y\right)}\)
d) \(\dfrac{1}{1-x}+\dfrac{1}{1+x}+\dfrac{2}{1+x^2}+\dfrac{4}{1+x^4}+\dfrac{8}{1+x^8}+\dfrac{16}{1+x^{16}}\)
\(=\dfrac{2}{1-x^2}+\dfrac{2}{1+x^2}+\dfrac{4}{1+x^4}+\dfrac{8}{1+x^8}+\dfrac{16}{1+x^{16}}\)
\(=\dfrac{4}{1-x^4}+\dfrac{4}{1+x^4}+\dfrac{8}{1+x^8}+\dfrac{16}{1+x^{16}}\)
.....
\(=\dfrac{16}{1-x^{16}}+\dfrac{16}{1+x^{16}}\)
\(=\dfrac{32}{1-x^{32}}\)

a: =>-4x>16
=>x<-4
c: =>20x-25<=21-3x
=>23x<=46
=>x<=2
d: =>20(2x-5)-30(3x-1)<12(3-x)-15(2x-1)
=>40x-100-90x+30<36-12x-30x+15
=>-50x-70<-42x+51
=>-8x<121
=>x>-121/8

a) (2x+12x−1−2x−12x+1):4x10x−5=(2x+1)2−(2x−1)2(2x−1)(2x+1).10x+54x(2x+12x−1−2x−12x+1):4x10x−5=(2x+1)2−(2x−1)2(2x−1)(2x+1).10x+54x
=4x2+4x+1−4x2+4x−1(2x−1)(2x+1).5(2x+1)4x4x2+4x+1−4x2+4x−1(2x−1)(2x+1).5(2x+1)4x
=8x.5(2x+1)(2x−1)(2
b) \(\left(\dfrac{1}{x^2+x}-\dfrac{2-x}{x+1}\right):\left(\dfrac{1}{x}+x-2\right)=\left(\dfrac{1}{x\left(x+1\right)}-\dfrac{x\left(2-x\right)}{x\left(x+1\right)}\right):\left(\dfrac{1}{x}+\dfrac{x^2}{x}-\dfrac{2x}{x}\right)=\left(\dfrac{1-2x+x^2}{x\left(x+1\right)}\right):\left(\dfrac{1+x^2-2x}{x}\right)=\left(\dfrac{\left(x-1\right)^2}{x\left(x+1\right)}\right)\cdot\left(\dfrac{x}{\left(x-1\right)^2}\right)=\dfrac{\left(x-1\right)^2\cdot x}{\left(x-1\right)^2\cdot x\cdot\left(x+1\right)}=\dfrac{1}{x+1}\)

bài này đề bài là chứng minh hay là giải bất phương trình vậy bạn

\(\left(\dfrac{2x}{2x+y}-\dfrac{4x^2}{4x^2+4xy+y^2}\right):\left(\dfrac{2x}{4x^2-y^2}+\dfrac{1}{y-2x}\right)\)
=\(\left[\dfrac{2x}{2x+y}-\dfrac{4x^2}{\left(2x+y\right)^2}\right]:\left[\dfrac{2x}{\left(2x-y\right)\left(2x+y\right)}-\dfrac{1}{2x-y}\right]\)
\(=\left[\dfrac{2x\left(2x+y\right)}{\left(2x+y\right)^2}-\dfrac{4x^2}{\left(2x+y\right)^2}\right]:\left[\dfrac{2x}{\left(2x-y\right)\left(2x+y\right)}-\dfrac{y+2x}{\left(2x-y\right)\left(y+2x\right)}\right]\)
\(=\left[\dfrac{4x^2+2xy-4x^2}{\left(2x+y\right)^2}\right]:[\dfrac{2x-y-2x}{\left(2x-y\right)\left(2x+y\right)}]\)
\(=\dfrac{2xy}{\left(2x+y\right)^2}:\dfrac{-y}{\left(2x-y\right)\left(2x+y\right)}\)
\(=\dfrac{2xy\left(2x-y\right)\left(2x+y\right)}{\left(2x+y\right)\left(2x+y\right)\left(-y\right)}\)
\(=\dfrac{2x\left(2x-y\right)}{-\left(2x+y\right)}\)
\(\dfrac{4x^2-2xy}{-2x-y}\)
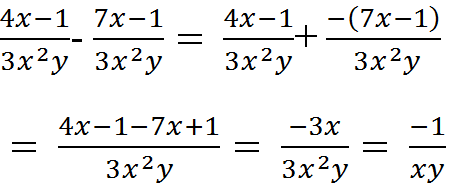
\(=\dfrac{4x^2+4x+1-4x^2+4x-1}{\left(2x-1\right)\left(2x+1\right)}\cdot\dfrac{5\left(2x-1\right)}{4x}\)
\(=\dfrac{8x}{4x}\cdot\dfrac{5}{2x+1}=\dfrac{10}{2x+1}\)