Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\frac{2^3.\left(0,5\right)^3.3^7}{2.\left(0,5\right)^4.3^8}=\frac{2^3.\left(\frac{1}{2}\right)^3.3^7}{2.\left(\frac{1}{2}\right)^4.3^8}=\frac{2^3.\frac{1^3}{2^3}.3^7}{2.\frac{1^4}{2^4}.3^8}=\frac{1.3^7}{\frac{1}{2^3}.3^8}=\frac{3^7}{\frac{3^8}{2^3}}=3^7.\frac{2^3}{3^8}=\frac{2^3}{3}=\frac{8}{3}\)

Ta có: \(0,4\left(3\right)=\dfrac{43-4}{90}=\dfrac{39}{90};\) \(0,6\left(2\right)=\dfrac{62-6}{90}=\dfrac{56}{90}\)
\(0,5\left(8\right)=\dfrac{58-5}{90}=\dfrac{53}{90}\)
Vậy biểu thức M có giá trị:
\(\dfrac{39}{90}+\dfrac{56}{90}.\dfrac{5}{2}-\dfrac{\dfrac{5}{6}}{\dfrac{53}{90}}.\dfrac{53}{30}=\dfrac{13}{30}+\dfrac{14}{9}-\dfrac{5}{6}.\dfrac{90}{53}.\dfrac{53}{50}=\dfrac{13}{30}+\dfrac{14}{9}-\dfrac{3}{2}\)
\(=\dfrac{13.9+14.30-3.135}{270}=\dfrac{402}{270}=\dfrac{67}{45}\)

\(P=\left(0,5-\dfrac{3}{5}\right):\left(-3\right)+\dfrac{1}{3}-\left(-\dfrac{1}{6}\right):\left(-2\right)\)
\(=\left(-\dfrac{1}{2}-\dfrac{3}{5}\right):\left(-3\right)+\dfrac{1}{3}-\left(-\dfrac{1}{6}\right).\left(-\dfrac{1}{2}\right)\)
\(=\left(\dfrac{-5-6}{10}\right):\left(-3\right)+\dfrac{1}{3}-\dfrac{1}{12}\)
\(=-\dfrac{11}{10}:\left(-3\right)+\dfrac{1}{4}\)
\(=-\dfrac{11}{10}.\left(-\dfrac{1}{3}\right)+\dfrac{1}{4}=\dfrac{11}{30}+\dfrac{1}{4}=\dfrac{37}{60}\)
Vậy \(P=\dfrac{37}{60}\)
\(Q=\left(\dfrac{2}{25}-1,008\right):\dfrac{4}{7}:\left[\left(3\dfrac{1}{4}-6\dfrac{5}{9}\right):2\dfrac{2}{17}\right]\)
\(=\left(\dfrac{2}{25}-\dfrac{126}{125}\right):\dfrac{4}{7}:\left[\left(\dfrac{13}{4}-\dfrac{59}{9}\right).\dfrac{36}{17}\right]\)
\(=-\dfrac{116}{125}.\dfrac{7}{4}:\left(-\dfrac{119}{36}.\dfrac{36}{17}\right)\)
\(=\dfrac{-29.7}{125}:\left(-7\right)=\dfrac{29}{125}\)
Vậy \(Q=\dfrac{29}{125}\)

\(\frac{2^{12}.3^5-4^6.9^2}{\left(2^2.3\right)^6+8^4.3^5}-\frac{5^{10}.7^3-25^5.49^2}{\left(125.7\right)^3+5^9.14^3}\)
\(=\frac{2^{12}.3^5-\left(2^2\right)^6.\left(3^2\right)^2}{2^{12}.3^6+\left(2^3\right)^4.3^5}-\frac{5^{10}.7^3-\left(5^2\right)^5.\left(7^2\right)^2}{\left(5^3.7\right)^3+5^9.\left(2.7\right)^3}\)
\(=\frac{2^{12}.3^5-2^{12}.3^4}{2^{12}.3^6+2^{12}.3^5}-\frac{5^{10}.7^3-5^{10}.7^4}{5^9.7^3+5^9.2^3.7^3}\)
\(=\frac{2^{12}.3^4\left(3-1\right)}{2^{12}.3^5\left(3+1\right)}-\frac{5^{10}.7^3.\left(1-7\right)}{5^9.7^3\left(1+2^3\right)}\)
\(=\frac{2^{12}.3^4.2}{2^{12}.3^5.4}-\frac{5^{10}.7^3.\left(-6\right)}{5^9.7^3.9}\)
\(=\frac{1}{6}-\frac{-10}{3}=\frac{1}{6}+\frac{10}{3}=\frac{1}{6}+\frac{20}{6}=\frac{21}{6}=\frac{7}{2}\)

f) \(\left(1:\frac{1}{7}\right)^2\left[\left(2^2\right)^3:2^5\right]\cdot\frac{1}{49}\)
\(=\left(1\cdot7\right)^2:\left(2^6:2^5\right)\cdot\frac{1}{49}=7^2\cdot\frac{1}{2}\cdot\frac{1}{49}=49\cdot\frac{1}{49}\cdot\frac{1}{2}=\frac{1}{2}\)
g) \(\frac{4^6\cdot3^5-2^{12}\cdot3^6}{2^{12}\cdot9^3+8^4\cdot3^5}=\frac{\left(2^2\right)^6\cdot3^5-2^{12}\cdot3^6}{2^{12}\cdot\left(3^2\right)^3+\left(2^3\right)^4\cdot3^5}\)
\(=\frac{2^{12}\cdot3^5-2^{12}\cdot3^6}{2^{12}\cdot3^6+2^{12}\cdot3^5}=\frac{2^{12}\left(3^5-3^6\right)}{2^{12}\left(3^6+3^5\right)}=\frac{2^{12}\left[3^5\left(1-3\right)\right]}{2^{12}\left[3^5\left(3+1\right)\right]}=\frac{2^{12}\cdot3^5\cdot\left(-2\right)}{2^{12}\cdot3^5\cdot4}=\frac{-2}{4}=-\frac{1}{2}\)
Bài giải
\(f,\text{ }\left(1\text{ : }\frac{1}{7}\right)^2\left[\left(2^2\right)^3\text{ : }2^5\right]\cdot\frac{1}{49}\)
\(=7^2\left(2^6\text{ : }2^5\right)\cdot\frac{1}{7^2}\)
\(=2\)
\(g,\text{ }\frac{4^6\cdot3^5-2^{12}\cdot3^6}{2^{12}\cdot9^3+8^4\cdot3^5}=\frac{2^{12}\cdot3^5-2^{12}\cdot3^6}{2^{12}\cdot3^6+2^{12}\cdot3^5}=\frac{2^{12}\cdot3^5\cdot\left(1-3\right)}{2^{12}\cdot3^5\cdot\left(3+1\right)}=-\frac{2}{4}=-\frac{1}{2}\)

\(A=\frac{2^{12}.3^5-4^6.9^2}{\left(2^2.3\right)^6+8^4.3^5}-\frac{5^{10}.7^3-25^5.49^2}{\left(125.7\right)^3+5^9.14^3}\)
\(\Rightarrow A=\frac{2^{12}.3^5-\left(2^2\right)^6.\left(3^2\right)^2}{2^{12}.3^6+\left(2^3\right)^4.3^5}-\frac{5^{10}.7^3-\left(5^2\right)^5.\left(7^2\right)^2}{\left(5^3.7\right)^3+5^9.\left(2.7\right)^3}\)
\(\Rightarrow A=\frac{2^{12}.3^5-2^{12}.3^4}{2^{12}.3^6+2^{12}.3^5}-\frac{5^{10}.7^3-5^{10}.7^4}{5^9.7^3+5^9.7^3.2^3}\)
\(\Rightarrow A=\frac{2^{12}.3^4\left(3-1\right)}{2^{12}.3^5\left(3+1\right)}-\frac{5^{10}.7^3\left(1-4\right)}{5^9.7^8\left(1+2^3\right)}\)
\(\Rightarrow A=\frac{2}{3.4}-\frac{5.\left(-3\right)}{9}\)
\(\Rightarrow A=\frac{1}{3}-\frac{-15}{9}\)
\(\Rightarrow A=\frac{1}{3}+\frac{5}{3}\)
\(\Rightarrow A=\frac{6}{3}=2\)
Vậy \(A=2\)

Sau khi thực hiện phép tính ta được kết quả các giá trị:
\(A=\dfrac{1}{3}\) \(B=-5\dfrac{5}{12}\) \(C=-0,22\)
Sắp xếp: \(-5\dfrac{5}{12}< -0,22< \dfrac{1}{3}\) tức là \(B< C< A\)
Khi tính xong giá trị biểu thức A , B và C ta được kết quả như sau :
\(A=\dfrac{1}{3}\) ; \(B=-5\dfrac{5}{12}\); \(C=-0,22\)
Sắp xếp : \(B< C< A\)\(\left(-5\dfrac{5}{12}< -0,22< \dfrac{1}{3}\right)\)
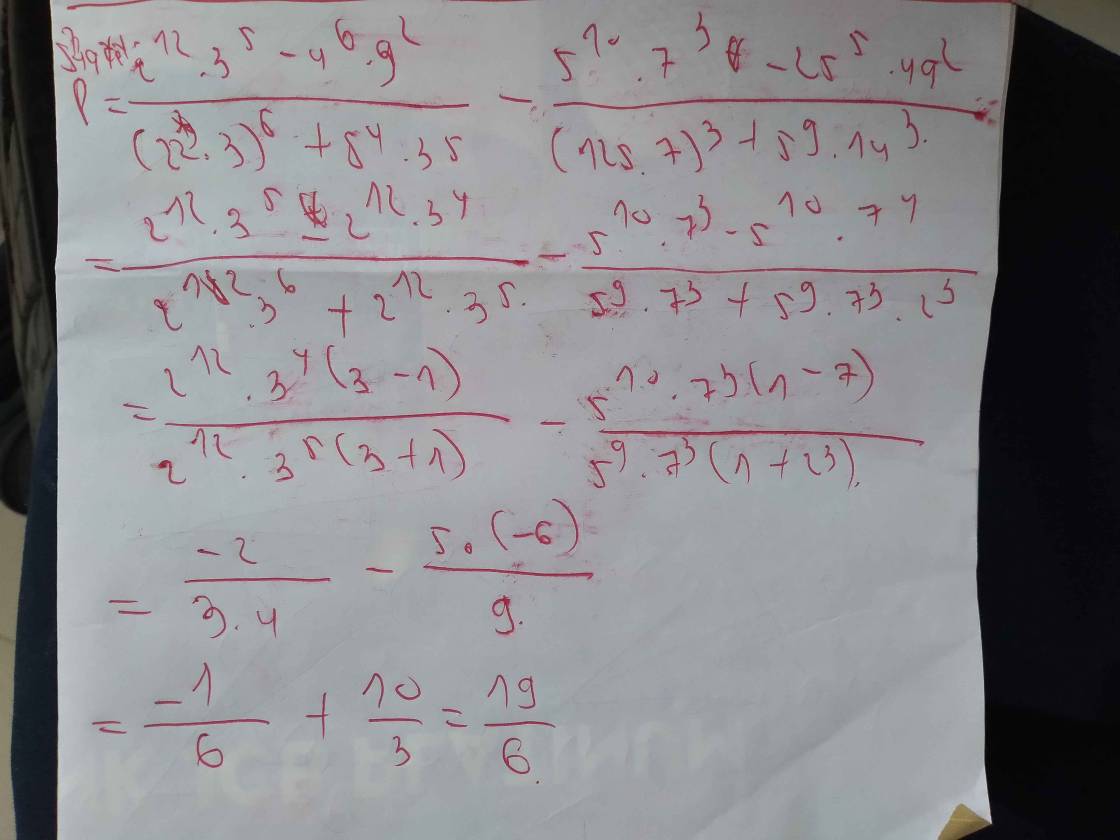
\(=\dfrac{\left(2\cdot0.5\right)^3\cdot3^7}{2\cdot\dfrac{16}{625}\cdot3^8}=\dfrac{1}{3}\cdot\dfrac{1}{\dfrac{32}{625}}=\dfrac{1}{3}\cdot\dfrac{625}{32}=\dfrac{625}{96}\)