
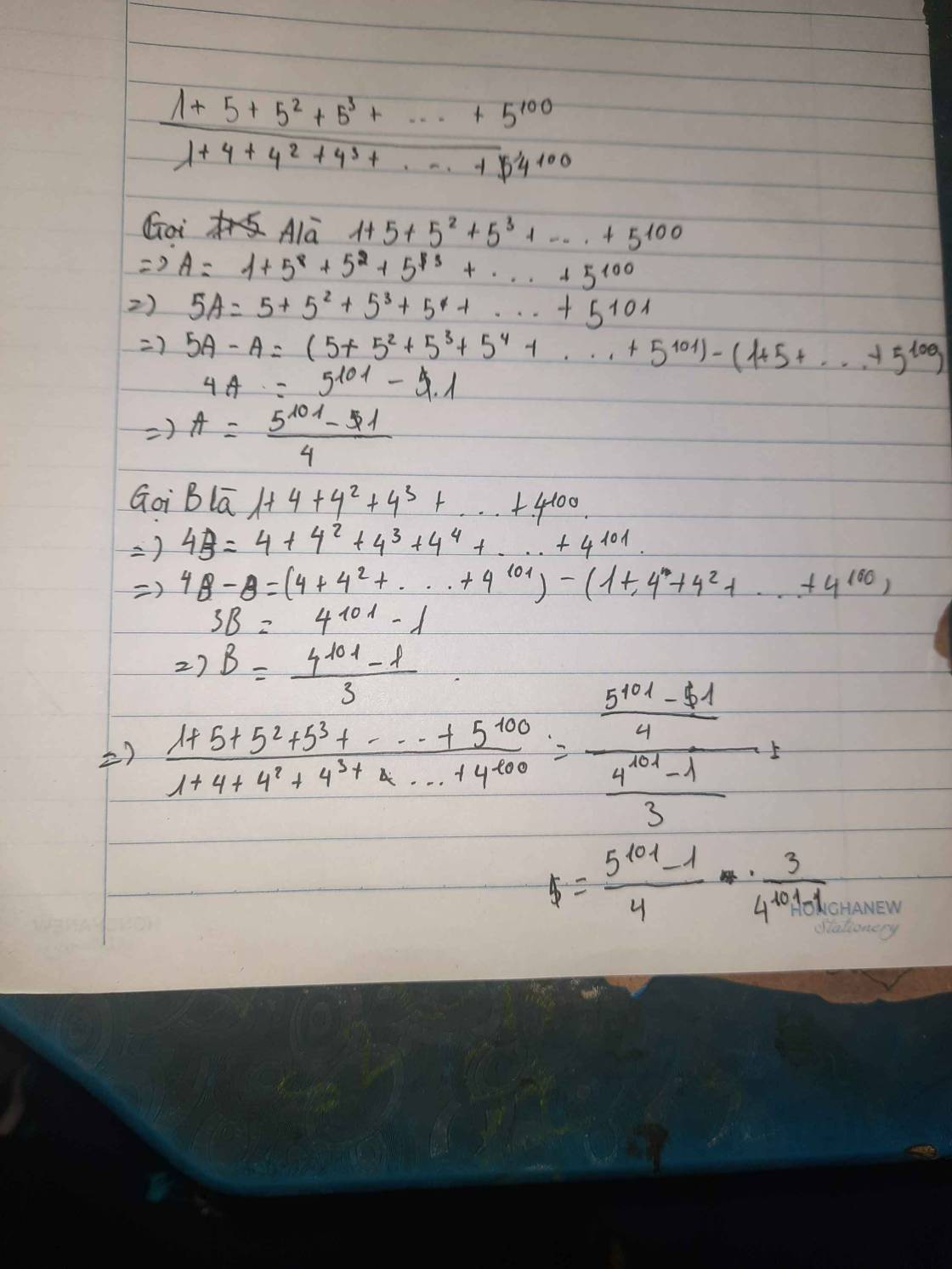
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

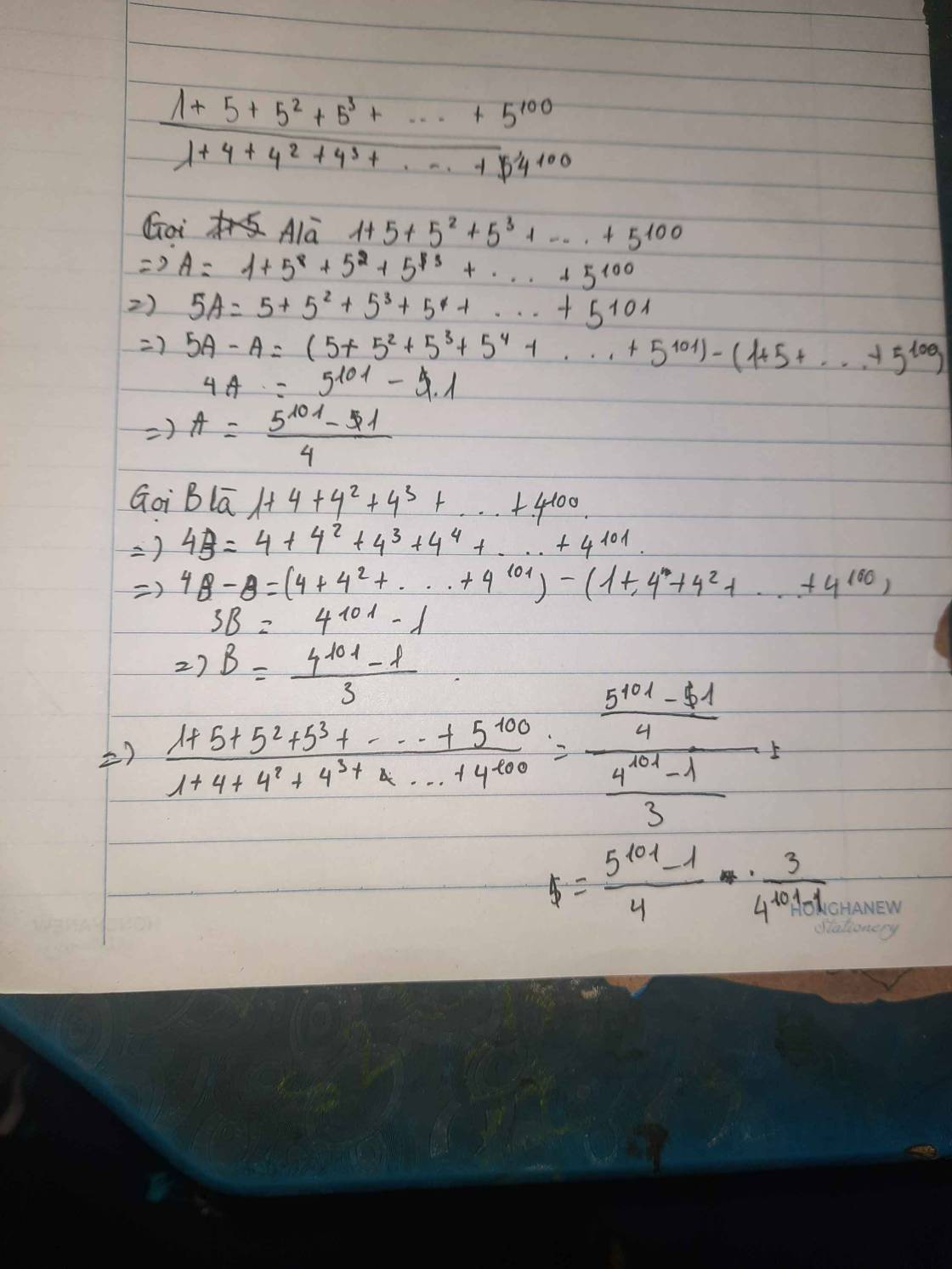

\(A=1+\dfrac{3}{2^3}+\dfrac{4}{2^4}+\dfrac{5}{2^5}+...+\dfrac{100}{2^{100}}\)
\(2A=2\left(1+\dfrac{3}{2^3}+\dfrac{4}{2^4}+\dfrac{5}{2^5}+...+\dfrac{100}{2^{100}}\right)\)
\(2A=2+\dfrac{3}{2^2}+\dfrac{4}{2^3}+\dfrac{5}{2^4}+....+\dfrac{100}{2^{99}}\)
\(2A-A=\left(2+\dfrac{3}{2^2}+\dfrac{4}{2^3}+\dfrac{5}{2^4}+...+\dfrac{100}{2^{99}}\right)-\left(1+\dfrac{3}{2^3}+\dfrac{4}{2^4}+\dfrac{5}{2^5}+...+\dfrac{100}{2^{100}}\right)\)\(A=2+\dfrac{3}{2^2}+\dfrac{1}{2^3}+\dfrac{1}{2^4}+...+\dfrac{1}{2^{99}}-\dfrac{100}{2^{100}}\)
\(A=\dfrac{11}{4}+\dfrac{1}{2^3}+\dfrac{1}{2^4}+...+\dfrac{1}{2^{99}}-\dfrac{100}{2^{100}}\)
\(A=\dfrac{11}{4}+\dfrac{1}{2^3}-\dfrac{1}{2^{99}}-\dfrac{100}{2^{100}}\)
Đặt \(D=1+\dfrac{3}{2^3}+\dfrac{4}{2^4}+...+\dfrac{100}{2^{100}}\)
\(2D=2+\dfrac{3}{2^2}+\dfrac{4}{2^3}+...+\dfrac{100}{2^{99}}\)
\(2D-D=\left(2+\dfrac{3}{2^2}+\dfrac{4}{2^3}+...+\dfrac{100}{2^{99}}\right)-\left(1+\dfrac{3}{2^3}+\dfrac{4}{2^4}+...+\dfrac{100}{2^{100}}\right)\)
\(D=2+\dfrac{3}{2^2}+\dfrac{1}{2^3}+....+\dfrac{1}{2^{99}}-\dfrac{100}{2^{100}}\)
\(D=\dfrac{11}{4}+\dfrac{1}{2^3}+...+\dfrac{1}{2^{99}}-\dfrac{100}{2^{100}}\)
\(D=\dfrac{11}{4}+\dfrac{1}{2^3}-\dfrac{1}{2^{99}}-\dfrac{100}{2^{100}}\)

\(A=1+\dfrac{3}{2^3}+\dfrac{4}{2^4}+..+\dfrac{100}{2^{100}}\\ \Rightarrow2A=2+\dfrac{3}{2^2}+\dfrac{4}{2^3}+...+\dfrac{100}{2^{99}}\\ \Rightarrow A=\dfrac{7}{4}+\dfrac{1}{2^3}+\dfrac{1}{2^4}+...+\dfrac{1}{2^{99}}-\dfrac{100}{2^{100}}\\ B=\dfrac{1}{2^3}+...+\dfrac{1}{2^{99}}\\ \Rightarrow2B=\dfrac{1}{2^2}+...+\dfrac{1}{2^{98}}\\ \Rightarrow B=\dfrac{1}{4}-\dfrac{1}{2^{99}}\\ \Rightarrow A=\dfrac{7}{4}+\dfrac{1}{4}-\dfrac{1}{2^{99}}-\dfrac{100}{2^{100}}\\ =2-\dfrac{1}{2^{99}}-\dfrac{100}{2^{100}}\)

2A =2+\(\frac{3}{2^2}\)+\(\frac{4}{2^3}\)+\(\frac{5}{2^4}\)+.....+\(\frac{100}{2^{99}}\)
\(\Rightarrow\)A=2A-A=1+\(\frac{3}{4}\)\(\frac{1}{2^3}\)+\(\frac{1}{2^4}\)+.....+\(\frac{1}{2^{99}}\)-\(\frac{100}{2^{100}}\)
\(\Rightarrow\)2A=2+\(\frac{3}{2}\)+\(\frac{1}{2^2}\)+\(\frac{1}{2^3}\)+....+\(\frac{1}{2^{98}}\)-\(\frac{100}{2^{99}}\)
\(\Rightarrow\)A=2A-A=1+\(\frac{3}{4}\)+\(\frac{1}{4}\)-\(\frac{101}{2^{99}}\)+\(\frac{100}{2^{100}}\)=2-\(\frac{51}{2^{99}}\)

\(A=1+\dfrac{3}{2^3}+\dfrac{4}{2^4}+...+\dfrac{100}{2^{100}}\)
\(\dfrac{1}{2}\cdot A=\dfrac{1}{2}+\dfrac{3}{2^4}+...+\dfrac{100}{2^{101}}\)
\(A-\dfrac{A}{2}=\dfrac{1}{2A}=\dfrac{1}{2}+\dfrac{3}{2^3}+...+\dfrac{100}{2^{101}}\)
\(\left[\dfrac{1}{2}+\dfrac{1}{2^2}+\dfrac{1}{2^3}+...+\dfrac{1}{2^{100}}\right]-\dfrac{100}{2^{101}}\) (do 3/2^3=1/2^2+1/2^3)
\(\left[1-\left(\dfrac{1}{2}\right)^{101}\right]\left(1-\dfrac{1}{2}\right)-\dfrac{100}{2^{101}}\)
\(\left(\dfrac{2^{101-1}}{2^{100}}\right)-\dfrac{100}{2^{101}}\)
\(\Rightarrow A=\dfrac{\dfrac{\left(2^{101-1}\right)}{2^{99}-100}}{2^{100}}\)

Giải:
\(A=1+\dfrac{3}{2^3}+\dfrac{4}{2^4}+\dfrac{5}{2^5}+...+\dfrac{100}{2^{100}}\)
\(\dfrac{1}{2}A=\dfrac{1}{2}+\dfrac{3}{2^4}+\dfrac{4}{2^5}+...+\dfrac{99}{2^{100}}+\dfrac{100}{2^{101}}\)
\(A-\dfrac{A}{2}=\dfrac{1}{2A}=\dfrac{1}{2}+\dfrac{3}{2^3}+\dfrac{1}{2^4}+...+\dfrac{1}{2^{100}}-\dfrac{100}{2^{101}}\)
\(=\left[\dfrac{1}{2}+\dfrac{1}{2^2}+\dfrac{1}{2^3}+...+\dfrac{1}{2^{100}}\right]-\dfrac{100}{2^{101}}\) ( Vì \(\dfrac{3}{2^3}=\dfrac{1}{2^2}+\dfrac{1}{2^3}\) )
\(=\dfrac{\left[1-\left(\dfrac{1}{2}\right)^{101}\right]}{\left(1-\dfrac{1}{2}\right)}-\dfrac{100}{2^{101}}\)
\(=\dfrac{\left(2^{101}-1\right)}{2^{100}}-\dfrac{100}{2^{101}}\)
\(\Rightarrow A=\dfrac{\left(2^{101}-1\right)}{2^{99}}-\dfrac{100}{2^{100}}\)

A=1+B
B=\(\Sigma\left(\dfrac{x}{2^x}\right)\)( cho x chạy từ 3 đến 100) =1
=> A=1+B=1+1=2![]()

\(A=1+\dfrac{3}{2^3}+\dfrac{4}{2^4}+.......+\dfrac{100}{2^{100}}\)
\(\Leftrightarrow2A=2+\dfrac{3}{2^2}+\dfrac{4}{2^3}+.........+\dfrac{100}{2^{99}}\)
\(\Leftrightarrow2A-A=\left(2+\dfrac{3}{2^2}+\dfrac{4}{2^3}+......+\dfrac{100}{2^{99}}\right)-\left(1+\dfrac{3}{2^3}+.........+\dfrac{100}{2^{100}}\right)\)
\(\Leftrightarrow A=\dfrac{11}{4}+\dfrac{1}{2^3}+\dfrac{1}{2^4}+......+\dfrac{1}{2^{99}}-\dfrac{100}{2^{100}}\)
Đặt :
\(H=\dfrac{1}{2^3}+\dfrac{1}{2^4}+......+\dfrac{1}{2^{99}}\)\(\Leftrightarrow A=\dfrac{11}{4}-H-\dfrac{100}{2^{100}}\)
\(\Leftrightarrow2H=\dfrac{1}{2^2}+\dfrac{1}{2^3}+........+\dfrac{1}{2^{98}}\)
\(\Leftrightarrow2H-H=\left(\dfrac{1}{2^2}+\dfrac{1}{2^3}+.....+\dfrac{1}{2^{98}}\right)-\left(\dfrac{1}{2^3}+\dfrac{1}{2^4}+.....+\dfrac{1}{2^{99}}\right)\)
\(\Leftrightarrow H=\dfrac{1}{2^2}-\dfrac{1}{2^{99}}\)
\(\Leftrightarrow A=\dfrac{11}{4}+\dfrac{1}{2^2}-\dfrac{1}{2^{99}}-\dfrac{100}{2^{100}}\)

\(linh=\dfrac{1}{5}+\dfrac{2}{5^2}+\dfrac{3}{5^3}+\dfrac{4}{5^4}+....+\dfrac{100}{5^{100}}\)
\(5linh=5\left(\dfrac{1}{5}+\dfrac{2}{5^2}+\dfrac{3}{5^3}+\dfrac{4}{5^4}+...+\dfrac{100}{5^{100}}\right)\)
\(5linh=1+\dfrac{2}{5}+\dfrac{3}{5^2}+\dfrac{4}{5^3}+...+\dfrac{100}{5^{99}}\)
\(5linh-linh=\left(1+\dfrac{2}{5}+\dfrac{3}{5^2}+\dfrac{4}{5^3}+...+\dfrac{100}{5^{99}}\right)-\left(\dfrac{1}{5}+\dfrac{2}{5^2}+\dfrac{3}{5^3}+\dfrac{4}{5^4}+...+\dfrac{100}{5^{100}}\right)\)
\(4linh=1+\dfrac{1}{5}+\dfrac{1}{5^2}+\dfrac{1}{5^3}+...+\dfrac{1}{5^{99}}-\dfrac{100}{5^{100}}\)
Đặt:
\(linh_2=1+\dfrac{1}{5}+\dfrac{1}{5^2}+\dfrac{1}{5^3}+....+\dfrac{1}{5^{99}}\)
\(5linh_2=5\left(1+\dfrac{1}{5}+\dfrac{1}{5^2}+\dfrac{1}{5^3}+....+\dfrac{1}{5^{99}}\right)\)
\(5linh_2=5+1+\dfrac{1}{5}+\dfrac{1}{5^2}+...+\dfrac{1}{5^{98}}\)
\(5linh_2-linh_2=\left(5+1+\dfrac{1}{5}+\dfrac{1}{5^2}+...+\dfrac{1}{5^{98}}\right)-\left(1+\dfrac{1}{5}+\dfrac{1}{5^2}+\dfrac{1}{5^3}+...+\dfrac{1}{5^{99}}\right)\)
\(4linh_2=5-\dfrac{1}{5^{99}}\)
\(linh=\dfrac{5}{4}-\dfrac{1}{5^{99}.4}\)
Nên \(4linh=\dfrac{5}{4}-\dfrac{1}{5^{99}.4}-\dfrac{100}{5^{100}}\)
Khi đó \(linh=\dfrac{5}{16}-\dfrac{1}{5^{99}.16}-\dfrac{100}{5^{100}.4}\)
Bài này bn dùng tính tổng xích ma trên máy tính:
\(\sum\limits^{100}_{x=1}\left(\dfrac{X}{5^X}\right)\)
Kết quả: 5/16