Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Fe được hòa tan hoàn toàn bởi dd HNO3 thu được dd X, khi thêm HCl vào X có khí NO thoát ra → trong X có ion Fe2+ → HNO3 đã phản ứng hết
n(NO) = 1,12/22,4 = 0,05mol
Fe + 4HNO3 → Fe(NO3)3 + NO + 4H2O
0,05___0,2______________0,05
Fe + 2Fe(NO3)3 → 3Fe(NO3)2
x___________________3x
Theo ĐL bảo toàn nguyên tố, số mol NO3- có trong muối:
n(NO3- trong muối) = n(HNO3) - n(NO) = 0,15mol
n(NaOH) = 0,115.2 = 0,23mol
Sau khi NaOH pư hoàn toàn với các chất trong dd Y, dung dịch thu được có:
n(Na+) = n(NaOH) = 0,23mol; n(Cl-) = n(HCl) = 0,1mol
→ n(NO3-) = n(Na+) - n(Cl-) = 0,23 - 0,1 = 0,13mol
→ Số mol NO3- bị Fe2+ khử: 0,15 - 0,13 = 0,02mol
NO3- + 3Fe2+ + 4H+ → 3Fe3+ + NO + 2H2O
0,02___0,06____0,08
NO3- và H+ đều dư (H+ dư 0,02mol) → Fe2+ đã phản ứng hết → 3x = 0,06 → x = 0,02mol
Tổng số mol Fe: n(Fe) = 0,05 + x = 0,07mol
Khối lượng Fe đã sử dụng: m(Fe) = 0,07.56 = 3,92g
TL:
Đốt cháy hh X cũng chính là đốt cháy C4H10 ban đầu.
C4H10 + O2 \(\rightarrow\) 4CO2 + 5H2O
0,1 0,4 0,5 mol
Sản phẩm cháy gồm 0,4 mol CO2 và 0,5 mol H2O. Khi hấp thụ vào nước vôi trong dư thì xảy ra phản ứng sau:
CO2 + Ca(OH)2 \(\rightarrow\) CaCO3 + H2O
0,4 0,4 mol
Như vậy khối lượng hấp thụ vào = 0,4.44 + 0,5.18 = 26,6 g. Khối lượng kết tủa tách ra khỏi dd = 0,4.100 = 40 g.
Do đó, khối lượng dd giảm = 40 - 26,6 = 13,4 g.
Số mol H3PO4: 0,050 x 0,50 = 0,025 (mol).
H3PO4 + 3NaOH → Na3PO4 + 3H2O
1 mol 3 mol
0,025 mol 3 x 0,025 mol
Thể tích dung dịch NaOH: 0,075 lít hay 75 ml
Số mol HCl = 0,016.1,25 = 0,02 mol.
a) Gọi V là thể tích nước cần thêm vào, ta có: 0,25.(V+16) = 0,02 hay V = 64 ml.
b) Sau khi trộn thu được thể tích là 96 ml. Do đó: 0,25.0,096 = 0,02 + 0,08a hay a = 0,05 M.
MgCO3 + 2HCl → MgCl2 + CO2 + H2O (1)
BaCO3 + 2HCl → BaCl2 + CO2 + H2O (2)
CO2 + Ca(OH)2 → CaCO3↓ + H2O. (3)
Theo (1), (2) và (3), để lượng kết tủa B thu được là lớn nhất thì:
nCO2 = nMgCO3 + nBaCO3 = 0,2 mol
Ta có: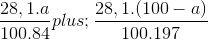 
= 0,2
=> a = 29,89.
Ta có:
Hàm \(\Psi\)được gọi là hàm chuẩn hóa nếu: \(\int\Psi.\Psi^{\circledast}d\tau=1hay\int\Psi^2d\tau=1\)
Hàm \(\Psi\)chưa chuẩn hóa là: \(\int\left|\Psi\right|^2d\tau=N\left(N\ne1\right)\)
Để có hàm chuẩn hóa, chia cả 2 vế cho N,ta có:
\(\frac{1}{N}.\int\left|\Psi\right|^2d\tau=1\Rightarrow\frac{1}{N}.\int\Psi.\Psi^{\circledast}d\tau=1\)
Trong đó: \(\Psi=\frac{1}{\sqrt{N}}.\Psi\)là hàm chuẩn hóa; \(\frac{1}{\sqrt{N}}\)là thừa số chuẩn hóa
Ta có:
\(\frac{1}{N}.\int\Psi.\Psi^{\circledast}d\tau=\frac{1}{N}.\int\left|\Psi\right|^2d\tau=1\Leftrightarrow\frac{1}{N}.\iiint\left|\Psi\right|^2dxdydz=1\)
Chuyển sang tọa độ cầu, ta có: \(\begin{cases}x=r.\cos\varphi.sin\theta\\y=r.sin\varphi.sin\theta\\z=r.\cos\theta\end{cases}\)với \(\begin{cases}0\le r\le\infty\\0\le\varphi\le2\pi\\0\le\theta\le\pi\end{cases}\)
\(\Rightarrow\frac{1}{N}.\iiint\left(r.\cos\varphi.sin\theta\right)^2.e^{-\frac{r}{a_o}}.r^2.sin\theta drd\varphi d\theta=1\)
\(\Leftrightarrow\frac{1}{N}.\int\limits^{\infty}_0r^4.e^{-\frac{r}{a_o}}dr.\int\limits^{2\pi}_0\cos^2\varphi d\varphi.\int\limits^{\pi}_0sin^3\theta d\theta=1\)
\(\Leftrightarrow\frac{1}{N}.\frac{4!}{\left(\frac{1}{a_o}\right)^5}.\int\limits^{2\pi}_0\frac{\cos\left(2\varphi\right)+1}{2}d\varphi\int\limits^{\pi}_0\frac{3.sin\theta-sin3\theta}{4}d\theta=1\)(do \(\int\limits^{\infty}_0x^n.e^{-a.x}dx=\frac{n!}{a^{n+1}}\))
\(\Leftrightarrow\frac{1}{N}.24.a^5_o.\frac{4}{3}.\pi=1\)
\(\Leftrightarrow\frac{1}{N}=\frac{1}{32.a^5_o.\pi}\)
\(\Rightarrow\)Thừa số chuẩn hóa là: \(\frac{1}{\sqrt{N}}=\sqrt{\frac{1}{32.a^5_o.\pi}}\); Hàm chuẩn hóa: \(\Psi=\frac{1}{\sqrt{N}}.\Psi=\sqrt{\frac{1}{32.a^5_o.\pi}}.x.e^{-\frac{r}{2a_o}}\)
áp dụng dk chuẩn hóa hàm sóng. \(\int\psi\psi^{\cdot}d\tau=1.\)
ta có: \(\int N.x.e^{-\frac{r}{2a_0}}.N.x.e^{-\frac{r}{2a_0}}.d\tau=1=N^2.\int_0^{\infty}r^4e^{-\frac{r}{a_0}}dr.\int_0^{\pi}\sin^3\theta d\tau.\int^{2\pi}_0\cos^2\varphi d\varphi=N^2.I_1.I_2.I_3\)
Thấy tích phân I1 có dạng tích phân hàm gamma. \(\int^{+\infty}_0x^ne^{-ax}dx=\int^{+\infty}_0\frac{\left(\left(ax\right)^{n+1-1}e^{-ax}\right)d\left(ax\right)}{a^{n+1}}=\frac{\Gamma\left(n+1\right)!}{a^{n+1}}=\frac{n!}{a^{n+1}}.\)
.áp dụng cho I1 ta được I\(I1=4!.a_0^5=24a^5_0\). tính \(I2=\int_0^{\pi}\sin^3\theta d\theta=\int_0^{\pi}\left(\cos^2-1\right)d\left(\cos\theta\right)=\frac{4}{3}\). tính tp \(I3=\int_0^{2\pi}\cos^2\varphi d\varphi=\int_0^{2\pi}\frac{\left(1-\cos\left(2\varphi\right)\right)}{2}d\varphi=\pi\)
suy ra \(\frac{N^2.24a_0^5.\pi.4}{3}=1\). vậy N=\(N=\frac{1}{\sqrt{32\pi a_0^5}}\). hàm \(\psi\) sau khi chiuẩn hóa có dạng \(\psi=\frac{1}{\sqrt{\pi32.a_0^5}}x.e^{-\frac{r}{2a_0}}\)
Câu 4
Gọi x là số mol Fe3O4; 3x là số mol CuO. Ta có: 80.3x + 232x = 4,72 thu được x = 0,01 mol.
Số mol CO và H2 = nO = nCuO + 4nFe3O4 = 0,03 + 0,04 = 0,07 mol. V = 1.568 lít.
Vì sao mà có được như vậy giải thích rõ hơn được không ạ
Số mol CO và H2 = nO = nCuO + 4nFe3O4 = 0,03 + 0,04 = 0,07 mol. V = 1.568 lít.
Đáp án C
H+ + OH– → H2O || Trung hòa ⇒ nOH– = nH+ = 0,01 mol.
⇒ x = 0,01 ÷ 0,05 = 0,2M