Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

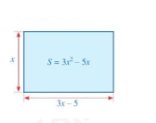
\(3{{\rm{x}}^2} - 5{\rm{x = x}}\left( {3{\rm{x}} - 5} \right)\)

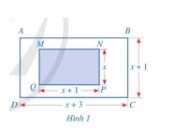
Biểu thức diện tích của hình chữ nhật ABCD là: \({S_{ABC{\rm{D}}}} = \left( {x + 1} \right)\left( {x + 3} \right)\)
Biểu thức diện tích của hình chữ nhật MNPQ là: \({S_{MNPQ}} = x\left( {x + 1} \right)\)
Tỉ số diện tích của hình chữ nhật ABCD và hình chữ nhật MNPQ là: \(\dfrac{{{S_{ABC{\rm{D}}}}}}{{{S_{MNPQ}}}} = \dfrac{{\left( {x + 1} \right)\left( {x + 3} \right)}}{{x\left( {x + 1} \right)}} = \dfrac{{x + 3}}{x}\)
b) Với x = 5 ta có: \(\dfrac{{{S_{ABC{\rm{D}}}}}}{{{S_{MNPQ}}}} = \dfrac{{5 + 3}}{5} = \dfrac{8}{5}\)
Với x = 2 ta có: \(\dfrac{{{S_{ABC{\rm{D}}}}}}{{{S_{MNPQ}}}} = \dfrac{{2 + 3}}{2} = \dfrac{5}{2}\)

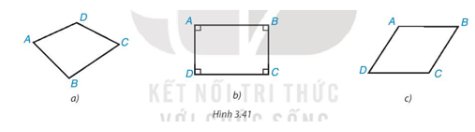
Tứ giác ABCD trong Hình 3.41b là hình chữ nhật vì có \(\widehat A = \widehat B = \widehat C = \widehat D = {90^o}\)
Tứ giác ABCD trong Hình 3.41a và Hình 3.41c không phải là hình chữ nhật vì không có 4 góc vuông.

Xét tứ giác ABCD có:
\(\begin{array}{l} \widehat A + \widehat B + \widehat C + \widehat D = {360^0}\\{85^0} + x + {65^0} + {75^0} = {360^0}\\x = {360^0} - {85^0} - {65^0} - {75^0} = {135^0}\end{array}\)

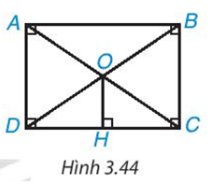
Xét tam giác DBC, ta có:
O là trung điểm cạnh BD (tính chất hình chữ nhật)
OH // BC (cùng vuông góc với CD)
⇒ OH là đường trung bình tam giác BCD.
⇒ H là trung điểm của CD (đpcm).

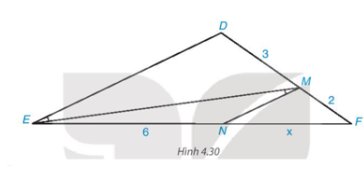
Trong Hình 4.30 có \(\widehat {DEM} = \widehat {EMN}\) mà hai góc này ở vị trí so le trong nên MN // DE.
Áp dụng định lí Thalès vào tam giác DEF có MN // DE, ta có:
\(\dfrac{{MF}}{{M{\rm{D}}}} = \dfrac{{NF}}{{NE}}\) hay \(\dfrac{2}{3} = \dfrac{x}{6}\)
Suy ra \(x = \dfrac{{2.6}}{3} = 4\) (đvđd).
Vậy x = 4 (đvđd).

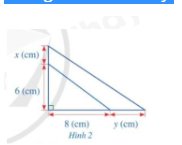
Diện tích hình tam giác vuông ban đầu là: \(\dfrac{1}{2}.6.8 = 24\left( {c{m^2}} \right)\)
Độ dài các cạnh của hình vuông sau khi tăng độ dài là: x + 6 (cm); y + 8 (cm)
Diện tích tam giác vuông sau khi tăng độ dài là: \(\dfrac{1}{2}\left( {x + 6} \right).\left( {y + 8} \right) = \dfrac{{{xy}}}{2} + 4x + 3y + 24\left( {c{m^2}} \right)\)
Đa thức biểu thị phần diện tích tăng thêm của miếng bìa là: \(\dfrac{{{xy}}}{2} + 4x + 3y + 24 - 24 = \dfrac{{{xy}}}{2} + 4x + 3y\left( {c{m^2}} \right)\)
Vậy đa thức biểu thị phần diện tích tăng thêm của miếng bìa là: \(\dfrac{{{xy}}}{2} + 4x + 3y\left( {c{m^2}} \right)\)

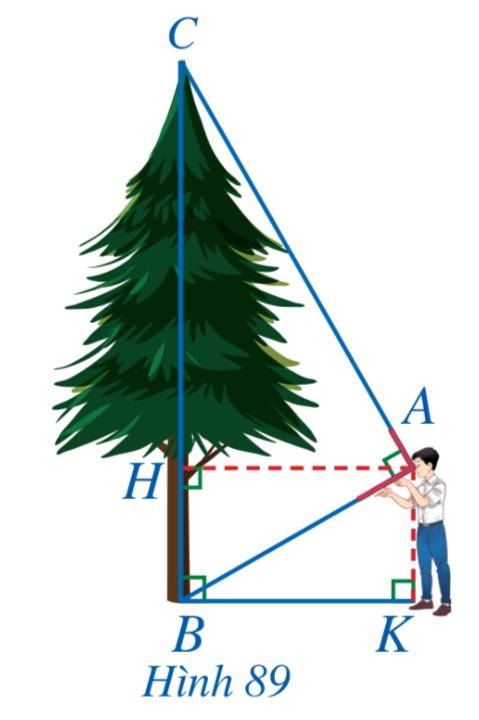
Xét tứ giác AHBK có \(\widehat H = \widehat B = \widehat K = 90^\circ \) nên AHBK là hình chữ nhật.
\( \Rightarrow AK = BH = 1,6m\)
Xét tam giác ABH vuông tại H có:
\(A{H^2} + H{B^2} = A{B^2}\) (Định lý Pytago)
\(\begin{array}{l} \Rightarrow 2,{8^2} + 1,{6^2} = A{B^2}\\ \Rightarrow A{B^2} = 10,4\\ \Rightarrow AB = \frac{{2\sqrt {65} }}{5}\end{array}\)
Xét tam giác ABC và tam giác HBA có:
\(\widehat {BAC} = \widehat {BHA} = 90^\circ \) và \(\widehat C\) chung
\( \Rightarrow \Delta ABC \backsim \Delta HBA\) (g-g)
\( \Rightarrow \frac{{BC}}{{BA}} = \frac{{AB}}{{HB}} \Leftrightarrow BC = A{B^2}:HB = {\left( {\frac{{2\sqrt {65} }}{5}} \right)^2}:1,6 = 6,5\)
Vậy cây cao 6,5m.

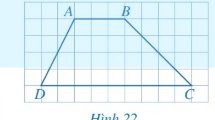
Hai cạnh AB và CD của tứ giác ABCD có song song với nhau.


Ta có:
V của hình HCN đó là:
`3x*y * 2x = 6x^2y`
Vậy, biểu thức biểu thị V của hình HCN đó là `6x^2y`
`=>` Biểu thức lập được của bạn Tâm là đúng.