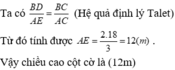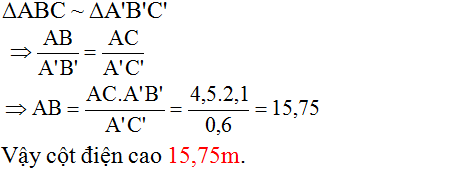Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

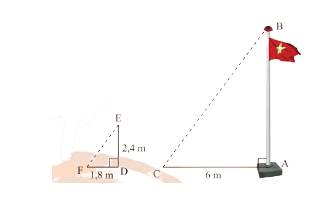
Cùng một thời điểm thì góc tạo bởi tia nắng và mặt đất là như nhau. Do đó, \(\widehat {EFD} = \widehat {BCA}\).
Xét tam giác \(DEF\) và tam giác \(ABC\) ta có:
\(\widehat {EFD} = \widehat {BCA}\) (chứng minh trên)
\(\widehat {EDF} = \widehat {BAC} = 90^\circ \).
Do đó, \(\Delta DEF\backsim\Delta ABC\) (g.g)
Suy ra, \(\frac{{FD}}{{AC}} = \frac{{ED}}{{AB}} \Leftrightarrow \frac{{1,8}}{6} = \frac{{2,4}}{{AB}} \Rightarrow AB = \frac{{6.2,4}}{{1,8}} = 8\).
Vậy cột cờ \(AB\) cao 8m.

Lời giải
Giả sử cột điện là AC, có bóng trên mặt đất là AB.
Thanh sắt là A'C', có bóng trên mặt đất là A'B'.
Vì cột điện và thanh sắt đều vuông góc với mặt đất nên hai tam giác ABC và A'B'C' đều là tam giác vuông.
Vì cùng một thời điểm tia sáng chiếu nên ta suy ra góc ACB = góc A'C'B'

Giải :
A' A B' B C' C 4,5 0,6 2,1 x
Gọi chiều cao cột điện là x (m).
Giả sử cột điện là AC, có bóng trên mặt đất là AB.
Thanh sắt là A'C', có bóng trên mặt đất là A'B'.
Vì cột điện và thanh sắt đều vuông góc với mặt đất nên hai tam giác ABC và A'B'C' đều là tam giác vuông.
Vì cùng một thời điểm tia sáng tạo với mặt đất một góc bằng nhau.
\(\Rightarrow\:\widehat{B}=\widehat{B'}\)
\(\Rightarrow\bigtriangleup ABC\:~ \bigtriangleup A'B'C' \)
\(\Rightarrow\frac{AC}{A'C'}=\frac{AB}{A'B'}\)
\(\Rightarrow\frac{x}{2,1}=\frac{4,5}{0,6}\)
\(\Rightarrow0,6x=2,1\cdot4,5\)
\(\Leftrightarrow0,6x=9,45\)
\(\Leftrightarrow x=\frac{9,45}{0,6}=15,75\:\left(m\right)\).