Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi số học sinh giỏi cả 3 môn Toán, Văn, Anh là \(x\left(x>0,x\in N^{\circledast}\right)\) (học sinh)
Số học sinh chỉ giỏi một môn Anh là: \(48-22-\left(15-x\right)\) (học sinh)
Số học sinh chỉ giỏi một môn Toán là: \(50-25-\left(22-x\right)\) (học sinh)
Số học sinh chỉ giỏi một môn Văn là: \(45-25-\left(15-x\right)\) (học sinh)
Theo bài ra ta có phương trình:
\(50-25-\left(22-x\right)+45-25-\left(15-x\right)+48-22-\left(15-x\right)=99-6\)
\(\Leftrightarrow50-25-22+x+45-25-15+x+48-22-15+x=93\)
\(\Leftrightarrow3x+19=93\)
\(\Leftrightarrow3x=74\Leftrightarrow x=\frac{74}{3}\left(kt/m\right)\)
Đề sai à ![]()

Gọi số học sinh lớp 8a đạt điểm 10 là x(bạn, x>0)
thì số học sinh lớp 8a là x/(5/7)= (7/5)x (bạn)
Nếu có thên 3 bạn đạt điểm 10 thì số bạn đạt điểm 10 là x+3 (bạn)
=> Số học sinh lớp 8a là (x+3)/80%= (x+3)/(4/5)= (5/4)(x+3)= (5/4)x+ 15/4 (bạn)
ta có phương trình (7/5)x= (5/4)x+ 15/4
<=> (3/20)x= 15/4
<=> x= (15/4)/(3/20)
<=> x= 25
x= 25 thoả mãn điều kiện của ẩn
=> Lớp 8a có 25 bạn được điểm 10
=> Số học sinh lớp 8a là: 25(7/5)= 35 bạn
**Vậy lớp 8a có 35 học sinh**

Gọi tổng số hs đi tham quan là x
Số hs khối 6 là \(\frac{2}{5}\)x
Số hs khối 7 là \(\frac{3}{4}.\frac{2}{5}x=\frac{3}{10}x\)
Vì shs khối 8 là 135 em , ta có pt :
x - \(\frac{2}{5}x-\frac{3}{10}x\) = 135 ⇌ 10x - 4x - 3x = 1350
⇌ 3x = 1350
⇌ x = 450
Vậy tổng số hs đi tham quan là 450 em

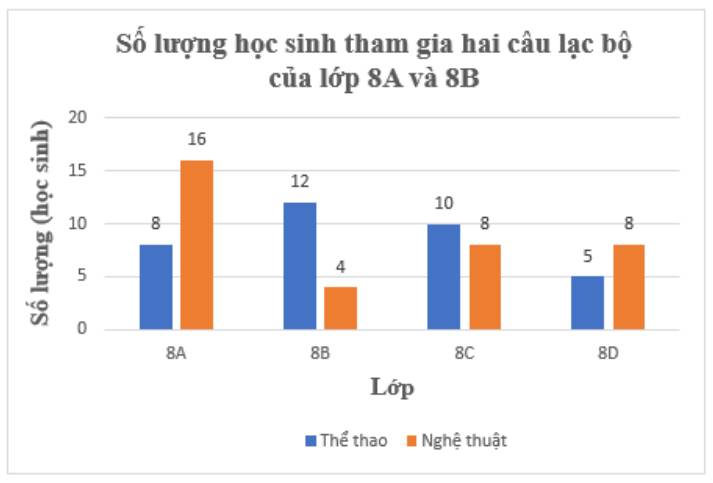
a) Để so sánh số lượng học sinh tham gia hai câu lạc bộ này ở từng lớp, ta chọn biểu đồ cột kép.
Biểu đồ cột kép biểu diễn số lượng của các lớp khối 8 tham gia các câu lạc bộ Thể thao và Nghệ thuật của trường như sau:
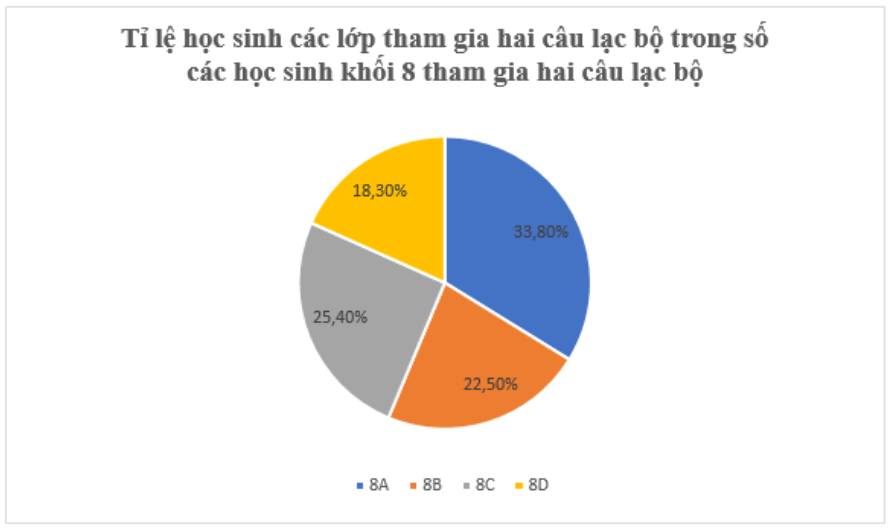
b) Để biểu diễn tỉ lệ học sinh các lớp tham gia hai câu lạc bộ trong số các học sinh khối 8 tham gia hai câu lạc bộ này ta dùng biểu đồ hình quạt tròn.
Tổng số học sinh tham gia hai câu lạc bộ của khối 8 là:
8 + 16 + 12 + 4 + 10 + 8 + 5 + 8 = 71 (học sinh).
• Tổng số học sinh tham gia hai câu lạc bộ của lớp 8A là: 8 + 16 = 24 (học sinh).
Tỉ số phần trăm số học sinh tham gia hai câu lạc bộ của lớp 8A so với số các học sinh khối 8 tham gia hai câu lạc bộ là: \(\frac{{24}}{{71}} \approx 33,8\% \) .
• Tổng số học sinh tham gia hai câu lạc bộ của lớp 8B là: 12 + 4 = 16 (học sinh).
Tỉ số phần trăm số học sinh tham gia hai câu lạc bộ của lớp 8B so với số các học sinh khối 8 tham gia hai câu lạc bộ là: \(\frac{{16}}{{71}} \approx 22,5\% \)
• Tổng số học sinh tham gia hai câu lạc bộ của lớp 8C là: 10 + 8 = 18 (học sinh).
Tỉ số phần trăm số học sinh tham gia hai câu lạc bộ của lớp 8C so với số các học sinh khối 8 tham gia hai câu lạc bộ là: \(\frac{{18}}{{71}} \approx 25,4\% \).
• Tỉ số phần trăm số học sinh tham gia hai câu lạc bộ của lớp 8C so với số các học sinh khối 8 tham gia hai câu lạc bộ là:
100% − 33,8% − 22,5% − 25,4% = 18,3%.
Biểu đồ hình quạt tròn biểu diễn tỉ lệ học sinh các lớp tham gia hai câu lạc bộ trong số các học sinh khối 8 tham gia hai câu lạc bộ này.

gọi điểm kiểm tra học kì của Tiến để đạt được hsg là x ( x>0) \(\Rightarrow\)theo đầu bài ta có tổng hệ số là 13 nên ta có phương trình sau :
\(\frac{9+9+9+6+8.2+8.2+9.2+3x}{13}\)= \(8\)
\(\Rightarrow\)75 + 3x = 104
\(\Rightarrow\)3x = 29
\(\Rightarrow\)x sấp sỉ 10 điểm thì thỏa mãn đk ủa ẩn và giúp điểm phảy trung bình của Đạt đạt loại giỏi
