Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn đáp án C
Do cuộn dây thuần cảm nên điện áp đặt vào hai đầu cuộn dây và cường độ dòng điện trong mạch biến đổi điều hòa và vuông pha với nhau.
Ta có phương trình 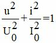
Đồ thị u(i) là đường elipse

Đáp án C.
Do cuộn dây thuần cảm nên điện áp đặt vào hai đầu cuộn dây và cường độ dòng điện trong mạch biến đổi điều hòa và vuông pha với nhau.
Ta có phương trình: 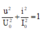
đồ thị u(i) là đường elipse.

\(U_{RC}=const=U\) khi \(Z_{L1}=2Z_C=R\)
Mặt khác L thay đổi để : \(U_{Lmax}:U_{Lmax}=\frac{U\sqrt{R^2+Z^2_C}}{R}=\frac{U\sqrt{2^2+1}}{2}=\frac{U\sqrt{5}}{2}\)
\(\Rightarrow chọn.D\)
+,có C=C1=>U_R=\frac{U.R}{\sqrt{R^2+(Zl-ZC1)^2}}
+,U R ko đổi =>Zl=ZC1
+,có c=C1/2=>ZC=2ZC1
=>U(AN)=U(RL)=\frac{U\sqrt{r^2+Z^2l}}{\sqrt{R^2+(Zl-2Z^2C1)}}=u=200V

Mạch chỉ có điện trở thuần thì u cùng pha với i.
Nếu \(u=U_0\cos\left(\omega t+\varphi\right)\)
Thì: \(i=I_0\cos\left(\omega t+\varphi\right)\)
\(\Rightarrow\frac{u}{U_0}=\frac{i}{I_0}\)
\(\Rightarrow\frac{u^2}{U_0^2}+\frac{i^2}{I_0^2}=1\) là sai.

\(2LC\omega^2=1\rightarrow2Z_L=Z_C\rightarrow2u_L=-uc\)
\(u_m=u_R+u_L+u_c=40+\left(-30\right)+60=70V\)
Chọn B

Đáp án C.
lúc đầu ta có :
UMB=2UR => ZMB=2R <=> ZC=\(\sqrt{3}\)R mà C=\(\frac{L}{R^2}\) => ZL=\(\frac{R}{\sqrt{3}}\)
lúc sau ta có Uc' max :
Zc'.ZL=R2+ \(Z^2_L\) => Zc'=\(\frac{4R}{\sqrt{3}}\)
\(\text{tanφ}=\frac{Z_L-Z_C}{R}\Rightarrow\tan\varphi=-\sqrt{3}\Rightarrow\varphi=-\frac{\pi}{3}\)

Điện áp giữ hai đầu đoạn mạch lệch pha \(\frac{\pi}{3}\) so với cường độ dòng điện:
\(\Rightarrow\cos\left(\frac{\pi}{3}\right)=\frac{R}{Z}\Leftrightarrow Z=80\Omega\)
Chọn đáp án C
Do cuộn dây thuần cảm nên điện áp đặt vào hai đầu cuộn dây và cường độ dòng điện trong mạch biến đổi điều hòa và vuông pha với nhau.