Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

OK, ZL mình vừa tính lúc nãy.
Giờ tìm \(\varphi\)
Ta có: \(\tan\varphi=\frac{Z_L-Z_C}{R}=\frac{\frac{4}{\sqrt{3}}R-\sqrt{3}R}{R}=\frac{1}{\sqrt{3}}\)
\(\Rightarrow\varphi=\frac{\pi}{6}\)
Vậy u sớm pha hơn i là \(\frac{\pi}{6}\)
Hay điện áp 2 đầu điện trở lệch pha \(\frac{\pi}{6}\)so với điện áp 2 đầu đoạn mạch.

\(U_{RC}=const=U\) khi \(Z_{L1}=2Z_C=R\)
Mặt khác L thay đổi để : \(U_{Lmax}:U_{Lmax}=\frac{U\sqrt{R^2+Z^2_C}}{R}=\frac{U\sqrt{2^2+1}}{2}=\frac{U\sqrt{5}}{2}\)
\(\Rightarrow chọn.D\)
+,có C=C1=>U_R=\frac{U.R}{\sqrt{R^2+(Zl-ZC1)^2}}
+,U R ko đổi =>Zl=ZC1
+,có c=C1/2=>ZC=2ZC1
=>U(AN)=U(RL)=\frac{U\sqrt{r^2+Z^2l}}{\sqrt{R^2+(Zl-2Z^2C1)}}=u=200V

Khi xảy ra cực đại của điện áp hiệu dụng trên cuộn dây, ta có U 2 = U L m a x U L m a x − U C → U = 80 V.
Đáp án A

Đáp án B
Phương pháp: Điều kiện cực trị khi tần số thay đổi.
Cách giải: Khi tần số góc thay đổi thì có các giá trị để điện áp trên cuộn cảm hay tụ đạt cực đại.
Ta có:
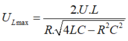
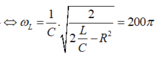
Và điện áp trên tụ cực đại là:
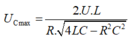
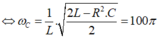
Dễ thấy:
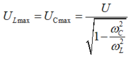
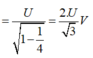

Đáp án B
Phương pháp: điều kiện cực trị khi tần số thay đổi.
Cách giải:
Khi tần số góc thay đổi thì có các giá trị để điện áp trên cuộn cảm hay tụ đạt cực đại. ta có:
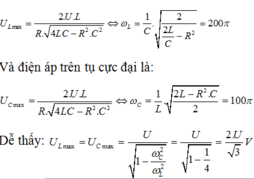

Đáp án A
+ Khi xảy ra cực đại của điện áp hiệu dụng trên hai đầu cuộn dây thì ô vuông pha với ![]()
→ Áp dụng hệ thức lượng trong tam giác, ta có
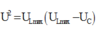
![]()

Khi U L cực đại thì điện áp tức thời giữa hai đầu đoạn mạch sẽ vuông pha với điện áp tức thời giữa hai đầu đoạn mạch chứa RC
→ U = U L m a x − U C U L m a x = 80 V.
Đáp án A