
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
TN
1

Các câu hỏi dưới đây có thể giống với câu hỏi trên

7 tháng 10 2016
\(x^3+y^3+xy=\left(x+y\right)^3-3xy\left(x+y\right)+xy=1-2xy\) (vì x+y=1)
Ta có \(P\) đạt giá trị lớn nhất khi \(1-2xy\) đạt giá trị nhỏ nhất \(\Leftrightarrow xy\) đạt giá trị lớn nhất
Mà x+y = 1 (tức tổng x,y không đổi) nên xy dạt giá trị lớn nhất khi x = y và x+y = 1 => x = y = 1/2 thay vào P được
\(MaxP=\frac{1}{\left(\frac{1}{2}\right)^3+\left(\frac{1}{2}\right)^3+\frac{1}{2}.\frac{1}{2}}=2\)
H
1

NV
Nguyễn Việt Lâm
Giáo viên
7 tháng 5 2023
\(P=\dfrac{6x+6y+2xy}{2}=\dfrac{6x+6y+2xy+10-10}{2}\)
\(=\dfrac{6x+6y+2xy+2\left(x^2+y^2\right)+6}{2}-5\)
\(=\dfrac{\left(x+y+2\right)^2+\left(x+1\right)^2+\left(y+1\right)^2}{2}-5\ge-5\)
\(P_{min}=-5\) khi \(x=y=-1\)


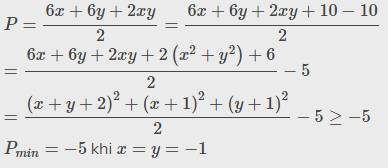
\(\left\{{}\begin{matrix}3^x=441\Rightarrow3=441^{\left(\dfrac{1}{x}\right)}\\7^y=441\Rightarrow7=441^{\left(\dfrac{1}{y}\right)}\end{matrix}\right.\)
\(\Rightarrow3.7=441^{\left(\dfrac{1}{x}\right)}.441^{\left(\dfrac{1}{y}\right)}\)
\(\Rightarrow21=441^{\left(\dfrac{1}{x}+\dfrac{1}{y}\right)}=21^{2\left(\dfrac{1}{x}+\dfrac{1}{y}\right)}\)
\(\Rightarrow2\left(\dfrac{1}{x}+\dfrac{1}{y}\right)=1\)
\(\Rightarrow2\left(\dfrac{x+y}{xy}\right)=1\)
\(\Rightarrow\dfrac{xy}{x+y}=2\)
\(\Rightarrow\left(\dfrac{xy}{x+y}\right)^2=4\)