Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Do tỉ số diện tích bằng bình phương tỉ số đồng dạng nên ta có:
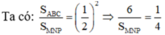
![]()

Vì ΔDEF ~ ΔABC theo tỉ số k 1 , ΔMNP ~ ΔDEF theo tỉ số k 2 nên ta có A B D E = k 1 ⇒ A B = k 1 . D E và M N D E = k 2 ⇒ M N = k 2 . D E
Từ đó ta có A B M N = D E k 1 k 2 . D E = 1 k 1 k 2 = 1 k 1 k 2
Đáp án: A

ΔABC~ΔMNP
=>\(\hat{B}=\hat{N};\hat{BAC}=\hat{NMP}\)
ta có: \(\hat{BAD}=\frac12\cdot\hat{BAC}\) (AD là phân giác của góc BAC)
\(\hat{NME}=\frac12\cdot\hat{NMP}\) (ME là phân giác của góc NMP)
mà \(\hat{BAC}=\hat{NMP}\)
nên \(\hat{BAD}=\hat{NME}\)
Xét ΔBAD và ΔNME có
\(\hat{BAD}=\hat{NME}\)
\(\hat{B}=\hat{N}\)
Do đó: ΔBAD~ΔNME
=>\(\frac{AD}{ME}=\frac{BA}{MN}=k\)

=>A
tỉ số đồng dạng bằng tỉ số chu vi, trung tuyến, phân giác, đường cao

ΔABC đồng dạng vơi ΔDEF theo hệ số tỉ lệ k=5/2
=>\(\dfrac{C_{ABC}}{C_{DEF}}=\dfrac{5}{2}\)
=>\(\dfrac{C_{ABC}}{5}=\dfrac{C_{DEF}}{2}=\dfrac{1890}{7}=270\)
=>\(C_{ABC}=1350\left(cm\right);C_{DEF}=540\)
Vì ΔABC ~ ΔDEF theo tỉ số k 1 , ΔMNP ~ ΔDEF theo tỉ số k 2 nên ta có A B D E = k 1 => A B = k 1 . D E và M N D E = k 2 => M N = k 2 . D E
Từ đó ta có A B M N = k 1 . D E k 2 . D E = k 1 k 2
Đáp án: D