cứu iemmmm
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
TT
5
NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
9 tháng 12 2022
Xét tg ABC có
\(\widehat{BAC}=180^o-\widehat{ABC}-\widehat{ACB}\) (tổng các góc trong của 1 tg \(=180^o\) )
\(\Rightarrow\widehat{BAC}=180^o-70^o-30^o=80^o=\widehat{ACD}\)
Hai góc \(\widehat{BAC}=\widehat{ACD}\) ở vị trí so le trong => AB//CD
QT
1
QT
1
HQ
Hà Quang Minh
Giáo viên
18 tháng 9 2023
Xét 2 tam giác ABC và MNP có:
AB=MN (gt)
\(\widehat {BAC} = \widehat {NMP}\) (gt)
AC=MP (gt)
Vậy \(\Delta ABC = \Delta MNP\)(c.g.c)
GN
GV Nguyễn Trần Thành Đạt
Giáo viên
17 tháng 5 2023
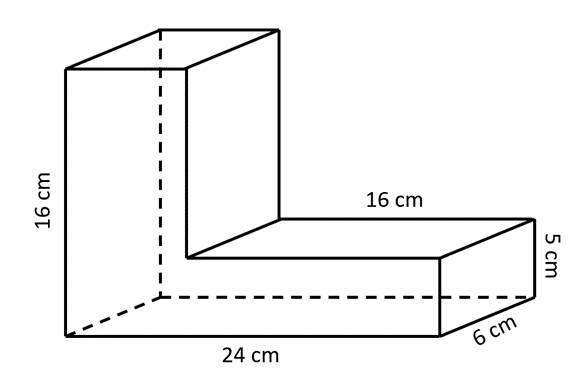
Chừ mình sẽ nối dài chiều dài của phần dưới của hình để được 2 HHCN.
Phần dưới có kích thước 24 x 6 x 5. Phần trên có kích thước là 8 x 6 x 11
a, Phần cần sơn là tổng diện tích toàn phần trừ đi 2 lần diện tích 8 x 6
Diện tích toàn phần HHCN trên:
2 x 8 x 6 + 2 x 11 x (8+6)= 404 (cm2)
Diện tích toàn phần HHCN dưới:
2 x 24 x 6 + 2 x 5 x (6+24)= 438(cm2)
Diện tích bề mặt khối gỗ cần sơn:
404 + 438 - 2 x 8 x 6= 746(cm2)
b, Thể tích phần trên khối gỗ:
8 x 6 x 11= 528(cm3)
Thể tích phần dưới khối gỗ:
24 x 6 x 5 = 720(cm3)
Thể tích của khối gỗ đã cho:
528 + 720 = 1248(cm3)
QT
1
18 tháng 9 2023
Em thấy bạn Vuông nói đúng
Để chứng minh điều này, ta có thể chỉ ra trường hợp 2 góc bằng nhau nhưng không đối đỉnh.
Ví dụ:
\(\widehat {{O_1}} = \widehat {{O_2}}\) nhưng hai góc này không đối đỉnh
KV
4 tháng 12 2023
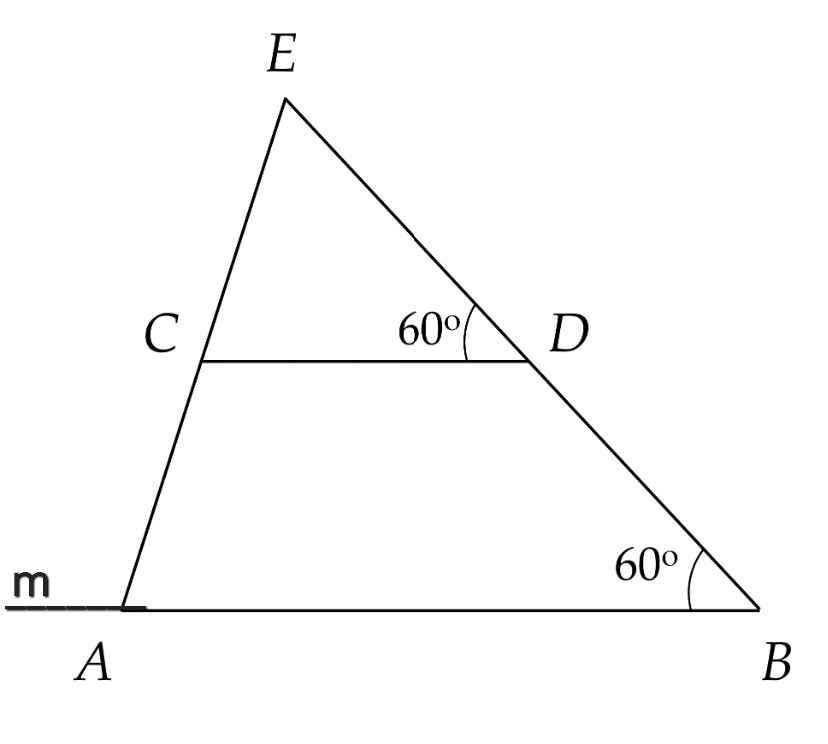
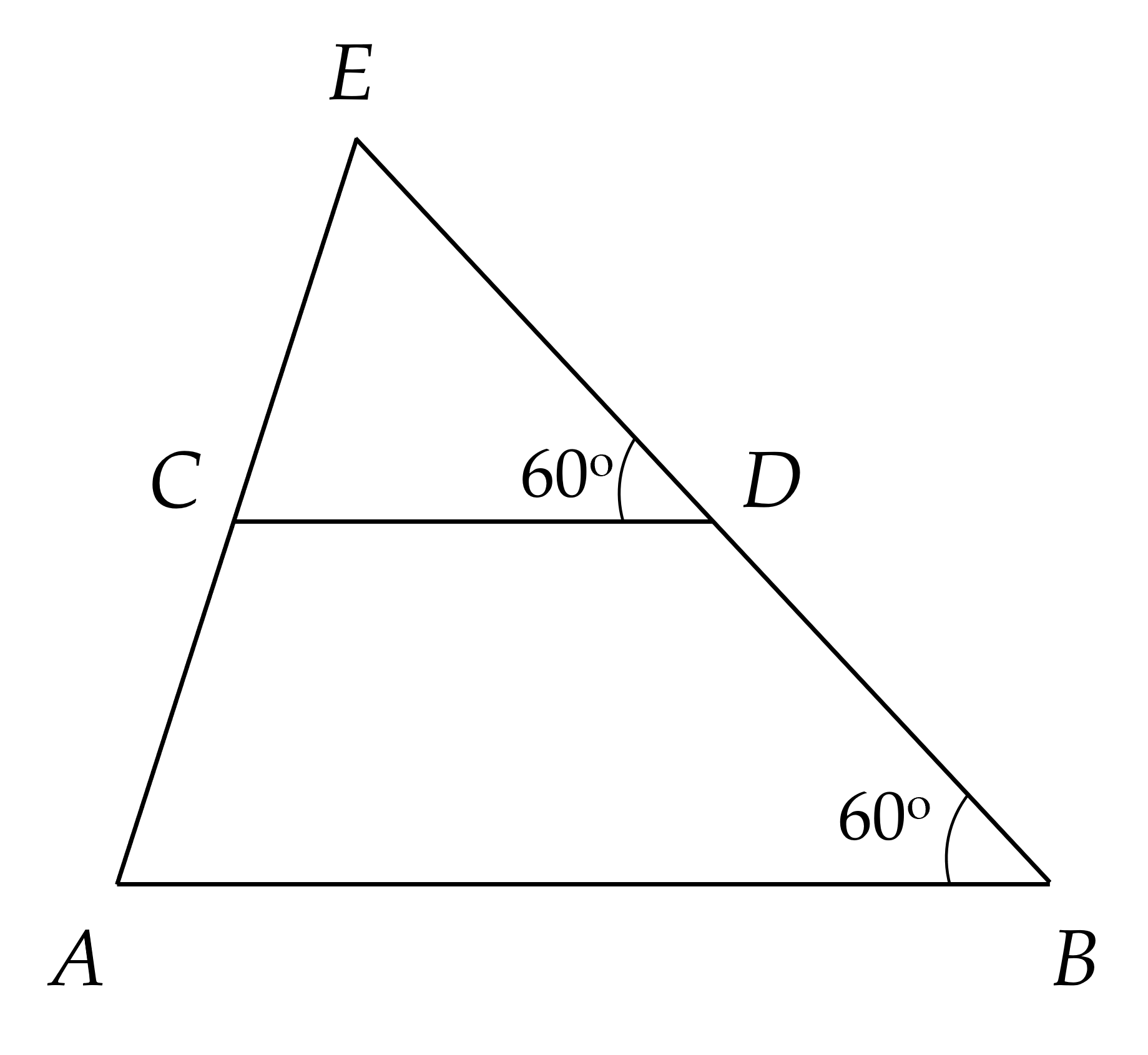
a) Ta có:
∠ABD = ∠CDE = 60⁰ (gt)
Mà ∠ABD và ∠CDE là hai góc so le trong
⇒ AB // CD
b) Vẽ tia Am là tia đối của tia AB
Do AB // CD
⇒ ∠mAC = ∠ACD (so le trong)
Mà ∠mAC + ∠BAC = 180⁰ (kề bù)
⇒ ∠ACD + ∠BAC = 180⁰
KV
25 tháng 1 2024
\(5x=3y\Rightarrow x=\dfrac{3y}{5}\)
Thay \(x=\dfrac{3y}{5}\) vào biểu thức \(x^2-y^2=-4\) ta có:
\(\left(\dfrac{3y}{5}\right)^2-y^2=-4\)
\(\dfrac{9y^2}{25}-y^2=-4\)
\(-\dfrac{16}{25}y^2=-4\)
\(y^2=-\dfrac{4}{\dfrac{-16}{25}}\)
\(y^2=\dfrac{25}{4}\)
\(\Rightarrow y=-\dfrac{5}{2};y=\dfrac{5}{2}\)
*) \(y=-\dfrac{5}{2}\Rightarrow x=\dfrac{3.\left(-\dfrac{5}{2}\right)}{5}=-\dfrac{3}{2}\)
*) \(y=\dfrac{5}{2}\Rightarrow x=\dfrac{3.\dfrac{5}{2}}{5}=\dfrac{3}{2}\)
Vậy ta được các cặp giá trị \(\left(x;y\right)\) thỏa mãn:
\(\left(-\dfrac{3}{2};-\dfrac{5}{2}\right);\left(\dfrac{3}{2};\dfrac{5}{2}\right)\)
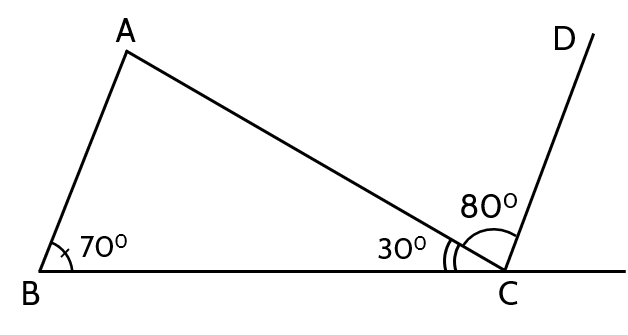
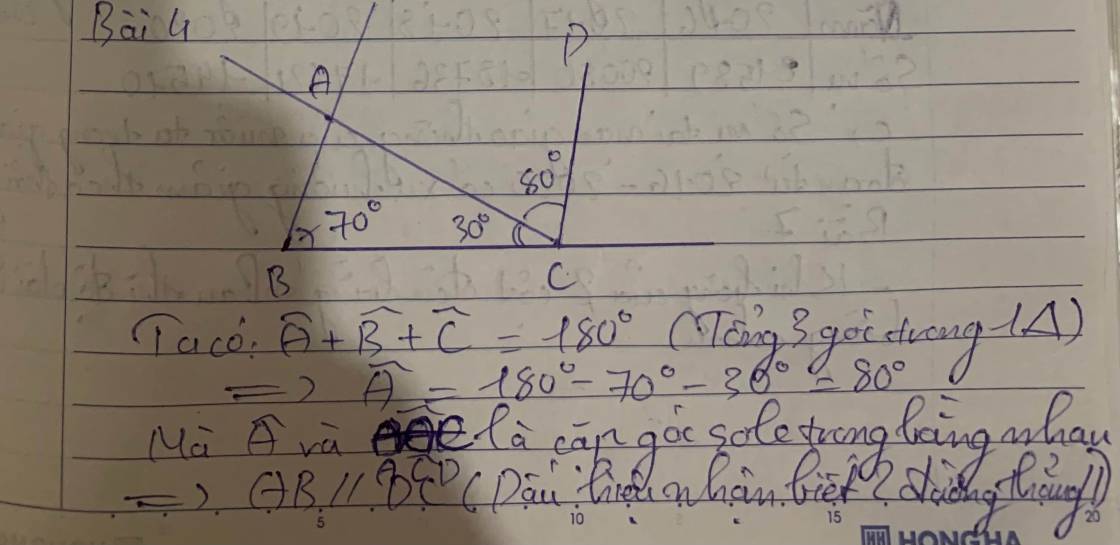
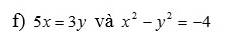
Lời giải:
Gọi tiền lãi ba đơn vị nhận được lần lượt là: $a,b,c$ (triệu đồng)
Theo bài ra ta có: $\frac{a}{3}=\frac{b}{4}=\frac{c}{7}$ và $a+b+c=980$
Áp dụng TCDTSBN:
$\frac{a}{3}=\frac{b}{4}=\frac{c}{7}=\frac{a+b+c}{3+4+7}=\frac{980}{14}=70$
$\Rightarrow a=70.3=210$ (triệu đồng); $b=70.4=280$ (triệu đồng); $c=70.7=490$ (triệu đồng)