Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Cường độ điện trường lớn nhất khi khoảng cách nhỏ nhất
\(\Rightarrow E_H\) nhỏ nhất với H là chân đường vuông góc hạ từ A xuống MN
Hơn nữa, do \(E_M=E_N\Rightarrow AM=AN\Rightarrow\Delta AMN\) vuông cân tại A
\(\Rightarrow AH=\frac{AM}{\sqrt{2}}\Rightarrow E_H=\frac{E_M}{\left(\frac{1}{\sqrt{2}}\right)^2}=2E_M=400\left(V/m\right)\)
tại sao \(AM\)=\(\dfrac{AM}{\sqrt{2}}\) ạ, và khúc sau là sao ạ, mong thầy rep comment ạ

Giả sử điện tích q đặt tại O như hình vẽ:
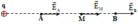
Ta có: E A = k q ε . O A 2 ; E B = k q ε . O B 2 ; E M = k q ε . O M 2
Vì M là trung điểm AB nên O M = O A + O B 2
Thay OA, OB, OM vào biểu thức trên ta được:
1 E M = 1 2 1 E A + 1 E B → E M = 4 E A E B E A + E B 2 = 16 V / m

E=K*Q/r^2 => 1.44r^2=9*10^9*1.6*10^-12 => r^2=0.01 =>r=0.1 =>r=10cm
quỹ tích là các tất cả các điểm nằm trên đường tròn có bk 10 cm
F=kq1q2/r^2 => F=9*10^9*1.6*10^-12*4*10^-12/0.1^2 => F=5.76*10^-12


