R
5
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
LV
20 tháng 4 2017
Đáp án và hướng dẫn giải bài 58:
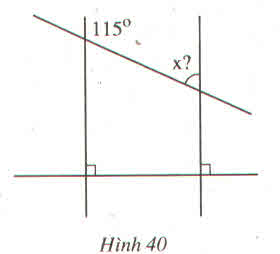
Ta có: a⊥c; b⊥c ⇒ a//b ( hai đường thẳng cùng vuông góc đường thẳng thứ ba)
⇒ ∠A + ∠B = 1800 (2 góc trong cùng phía)
⇒ 1150 + ∠B = 1800
⇒∠B = 650
.
5 tháng 10 2017
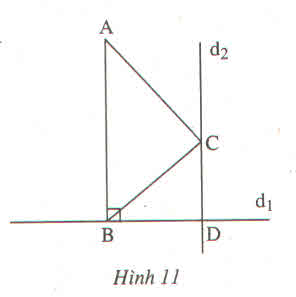
- Vẽ ∆ABC
- Vẽ đường thẳng d1 đi qua B và vuông góc với AB
- Vẽ đường thẳng d2 đi qua C và vuông góc với AB
- Gọi D là giao điểm của d1 và d2
Câu hỏi: Tại sao BDC=90o?
SG
2
SG
8
20 tháng 4 2017
|
Câu |
Đúng |
Sai |
|
1.Trong một tam giác, góc nhỏ nhất là góc nhọn |
x |
|
|
2.Trong một tam giác, có ít nhất là hai góc nhọn |
x |
|
|
3.Trong một tam giác, góc lớn nhất là góc tù |
|
x |
|
4.Trong một tam giác vuông, hai góc nhọn bù nhau |
|
x |
|
5. Nếu ˆAA^ là góc ở đáy của một tam giác cân thì ˆAA^ < 900 |
x |
|
|
6.Nếu ˆAA^ là góc ở đỉnh của một tam giác cân thì ˆAA^ < 900 |
|
x |
SG
2
TP
19 tháng 4 2017
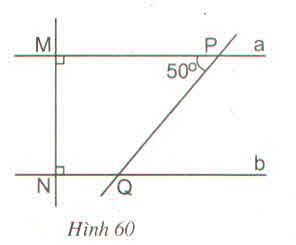
a) Hai đường thẳng a và b cùng vuông góc với đường thẳng MN nên a // b.
b) Ta có góc MPQ = góc Q1 = 50o (so le trong vì a // b)
mà góc Q1 + Q2 = 180o (kề bù)
=> Q2 = 180o - 50o = 130o
Vậy góc NQP = 130o.
D
19 tháng 4 2017
Kí hiệu như hình vẽ.
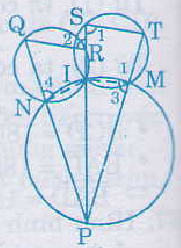
Ta có tứ giác ISTM nội tiếp đường tròn nên:
ˆS1S1^ + ˆMM^ = 180o
Mà ˆM1M1^ + ˆM3M3^ = 180o (kề bù)
nên suy ra ˆS1S1^ = ˆM3M3^ (1)
Tương tự từ các tứ giác nội tiếp IMPN và INQS ta được
ˆM3M3^ = ˆN4N4^ (2)
ˆN4N4^ = ˆR2R2^ (3)
Từ (1), (2), (3) suy ra
Do đó QR // ST
SG
3
LD
12 tháng 3 2018
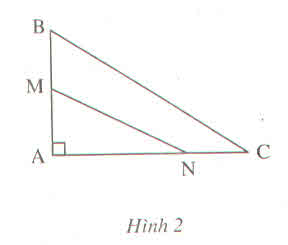
Hình chiếu của AN < hình chiếu của AC
=> đường xiên BN < đường xiên của BC (1)
Hình chiếu của AM < hình chiếu AB => đường xiên MN < đường xiên NB. (2)
Từ (1) và (2) suy ra:
MN< BN< BC.
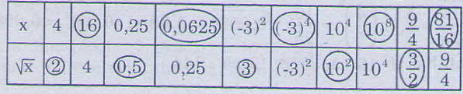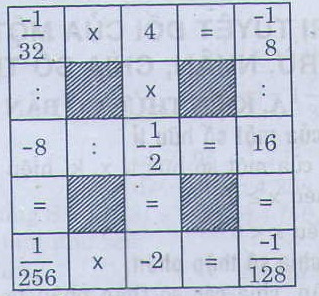
D
D. 450