Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn gốc thế năng tại VT dây thẳng đứng.
Áp dụng định luật bảo toàn năng lượng ta có:
\(W=mgl\left(1-\cos\alpha_0\right)=W_d+W_t=W_d+mgl\left(1-\cos\alpha\right)\)
\(\Rightarrow W_d=mgl\left(1-\cos\alpha_0-1+\cos\alpha\right)=mgl\left(\frac{\alpha^2_0}{2}-\frac{\alpha^2}{2}\right)\)
\(=0,1.10.0,8.\left(\frac{\left(\frac{8}{180}\pi\right)^2-\left(\frac{4}{180}\pi\right)^2}{2}\right)\approx5,84\left(mJ\right)\)

Dùng bảo toàn cơ năng lớp 10! đề không sai !
Với biên độ góc là 600 vẽ hình sẽ thấy độ cao
Nên:

Vật thực hiện 10 dao động mất 20s:
\(T=\frac{t}{n}=2s\Rightarrow g=4\pi^2\frac{l}{T^2}=9,86m/s^2\)
Đáp án C

Ta có: \(v=\omega\sqrt{s^2_0-s^2}=\sqrt{gl\left(\alpha^2_0-a^2_1\right)}\)\(=0,271\left(m\right)=27,1\left(cm\text{/}s\right)\)

Do E và B biến thiên cùng pha nên, khi cảm ứng từ có độ lớn B0/2 thì điện trường E cũng có độ lớn E0/2.
Bài toán trở thành tính thời gian ngắn nhất để cường độ điện trường có độ lớn E0/2 đang tăng đến độ lớn E0/2.
E M N Eo Eo/2
Từ giản đồ véc tơ quay ta dễ dang tính được thời gian đó là t = T/3
Suy ra: \(t=\dfrac{5}{3}.10^{-7}\)s

Đáp án A
Con lắc chịu hai sự biến đổi: sự nở dài về nhiệt và sự thay đổi độ cao.
Ta có:
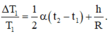
Theo đề bài, đồng hồ chạy đúng giờ nên

Suy ra
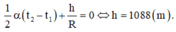

Ta có :
\(A=l'=\frac{mg}{k}=\frac{g}{\omega^2}\)
\(v_0=A\omega\Rightarrow\frac{g}{\omega}=v_0\Rightarrow\omega=\frac{g}{v_0}\)
\(\Rightarrow A=\frac{g}{\omega^2}=\frac{v^2_0}{g}=6,25\left(cm\right)\)

\(A=l'=\frac{mg}{k}=\frac{g}{\omega^2}\)
\(v_0=A\omega\Rightarrow\frac{g}{\omega}=v_0\Rightarrow\omega=\frac{g}{v_0}\)
\(\Rightarrow A=\frac{g}{\omega^2}=\frac{v^2_0}{g}=6,25\left(cm\right)\)

 =2 7,1 cm/s
=2 7,1 cm/s
Chọn A
+ Đồng hồ chạy đúng khi tổng các sai lệch về chu kỳ bằng 0:
=>