Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

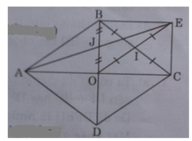
b)Ta có OA = OC (tính chất đường chéo hình thoi)
Mà OC = BE và OC // BE (cmt) nên OA = BE và OA // BE.
Do đó ABEO là hình bình hành
Ta có J là trung điểm của OB nên đường chéo thứ hai AI phải qua J và JA = JE.
⇒ E đối xứng với A qua trung điểm J của đoạn OB.

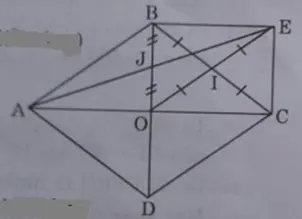
a) Ta có IB = IC (gt), IO = IE (tính chất đối xứng)
⇒ OBEC là hình bình hành.
Lại có ∠BOC = 90o (tính chất hai đường chéo hình thoi).
Do đó OBEC là hình chữ nhật.
b)Ta có OA = OC (tính chất đường chéo hình thoi)
Mà OC = BE và OC // BE (cmt) nên OA = BE và OA // BE.
Do đó ABEO là hình bình hành
Ta có J là trung điểm của OB nên đường chéo thứ hai AI phải qua J và JA = JE.
⇒ E đối xứng với A qua trung điểm J của đoạn OB.
A B C D O E I J
a, Xét tứ giác OBEC,
I là trung điểm BC, OI= IE
=> OBEC là hình bình hành
mà \(\widehat{BOC}=90^0\) ( Vì ABCD là hình thoi)
=> OBEC là hình chữ nhật
b,OBEC là hình chữ nhật => BE =OC ; BE//OC
mà OC =AO
=> BE = AO , BE//AO
=> ABEO là hình bình hành
=> Hai đg chéo cắt nhau tại trung điểm mỗi đươngf
mà J là trung điểm OB => J là trung điểm AE
=> E đối xứng A qua J

Bài này có gì đâu em ! Anh làm nhé !
Chuyển vế cái cần chứng minh ta được
1/AB^2 - 1/AE^2 =1/4AF^2
hay ( AE^2 - AB^2)/AB^2.AE^2 = 1/4AF^2
hay BE^2/ 4BC^2.AE^2 = 1/AF^2
Nhân chéo hai vế ta có : BC.AE = BE.AF hay là BC/AF = BE/AE

1: Xét ΔACE có
I là trung điểm của AE
O là trung điểm của AC
Do đó: IO là đường trung bình của ΔACE
Suy ra: IO//CE
hay OIEC là hình thang

1.trong tam giác ADK :
AB=BD (D đối xứng vs A qua B)
N là trung điểm của AK
=>BN là đg trung bình của tam giác ADK
=> BN//DK
=>BN//MK
trong tam giác NBC có:
BN//MK
M là trung điểm của BC
=>NK=KC
mà NK=AN
=>AN=NK=KC
=>2NA=NC
a: Xét tứ giác OBEC có
I là trung điểm của BC
I là trung điểm của OE
Do đó:OBEC là hình bình hành
mà \(\widehat{BOC}=90^0\)
nên OBEC là hình chữ nhật
b: Xét tứ giác ABEO có
AO//BE
AO=BE
Do đó: ABEO là hình bình hành
Suy ra: Hai đường chéo AE và BO cắt nhau tại trung điểm của mỗi đừong
=>J là trung điểm của EA(đpcm)