Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Theo hệ thức Vi-ét ta có: x 1 + x 2 =13
Suy ra 12,5 + x 2 = 13 ⇔ x 2 = 0,5
Cũng theo hệ thức Vi-ét ta có: x 1 x 2 = m
Suy ra: m = 12,5.0,5 ⇔ m =6,25
Vậy với m = 6,25 thì phương trình x 2 -13x + m = 0 có hai nghiệm
x 1 =12,5 , x 2 =0,5

Theo hệ thức Vi-ét ta có: x 1 x 2 =-35
Suy ra 7 x 2 =-35 ⇔ x 2 =-5
Cũng theo hệ thức Vi-ét ta có: x 1 + x 2 =-m
Suy ra: m=-7 +5 ⇔ m =-2
Vậy với m =-2 thì phương trình x 2 + mx - 35 = 0 có hai nghiệm x 1 =7, x 2 =-5

Theo hệ thức Vi-ét ta có: x 1 + x 2 = - 3/4
Suy ra: -2 + x 2 = - 3/4 ⇔ x 2 = -3/4 + 2 = 5/4
Cũng theo hệ thức Vi-ét ta có: x 1 x 2 = (- m 2 +3m)/4
Suy ra: -2. 5/4 = (- m 2 +3m)/4 ⇔ m 2 -3m -10 =0
∆ = - 3 2 -4.1.(-10) =9+40 =49
∆ = 49 =7
m 1 =(3 +7)/(2.1) =5 ; m 2 =(3 -7)/(2.1) =-2
Vậy với m =5 hoặc m = -2 thì phương trình 4 x 2 +3x – m 2 +3m = 0 có hai nghiệm x 1 =-2 , x 2 =5/4

Theo hệ thức Vi-ét ta có: x 1 x 2 =5/3
Suy ra: 1/3 . x 2 = 5/3 ⇔ x 2 =5/3 : 1/3 =5/3 .3=5
cũng theo hệ thức Vi-ét ta có: x 1 + x 2 =[2(m -3)]/3
Suy ra: 1/3 +5 = [2(m -3)]/3 ⇔ 2(m -3) =16 ⇔ m-3=8 ⇔ m=11
Vậy với m = 11 thì phương trình 3 x 2 -2(m -3)x +5 =0 có hai nghiệm x 1 = 1/3 , x 2 = 5

Áp dụng vi-et ta suy ra được nghiệm là:
\(\hept{\begin{cases}x=\frac{-m-\sqrt{m^2-4n}}{2}\\x=\frac{-m+\sqrt{m^2-4n}}{2}\end{cases}}\)
Ta có:
\(x_1=x_2^2+x_2+2\)
\(\Leftrightarrow x_1+x_2=\left(x_2+1\right)^2+1\)
\(\Leftrightarrow-m=\left(x_2+1\right)^2+1\)
Với \(\hept{\begin{cases}x_2=\frac{-m-\sqrt{m^2-4n}}{2}\\n=6-m\end{cases}}\)
\(\Leftrightarrow-m=\frac{\left(m-2\right)\sqrt{m^2+4m-24}+m^2-10}{2}+1\)
\(\Leftrightarrow-2m-m^2+8=\left(m-2\right)\sqrt{m^2+4m-24}\)
\(\Leftrightarrow4m^3+24m^2-144m+160=0\)
\(\Leftrightarrow\orbr{\begin{cases}m=-10\\m=2\left(l\right)\end{cases}}\)
Tương tự cho trường hợp còn lại.

Ta có: −4x2 + 9 = 0 ⇔ 4x2 = 9
⇔ x 2 = 9 4 ⇔ x = 3 2 x = − 3 2
phương trình có hai nghiệm
x = 3 2 ; x = − 3 2
Đáp án cần chọn là: D

phương trình có a = 7 khác 0 => là phương trình bậc 2
vậy phương trình có nghiệm <=> \(\Delta'\ge0\Leftrightarrow\left(m-1\right)^2-7.\left(-m^2\right)\ge0\Leftrightarrow\left(m-1\right)^2+7m^2\ge0\)(thỏa mãn với mọi m)
b) theo vi et ta có
+) x1+x2 = -b/a = 2(m-1)/7
+) x1.x2 = c/a = -m2/7
a) Ta có : a = 7 ; b = 2(m-1) ; c = -m2
\(\Rightarrow\Delta'=\left(m-1\right)^2+7m^2\)
Do \(\left(m-1\right)^2\ge0\)mọi m và \(m^2\ge0\)mọi m
\(\Rightarrow\Delta'\ge0\)với mọi giá trị của m
Do đó PT có nghiệm với mọi giá trị của m
b) Gọi 2 nghiệm của PT là x1 ; x2
Theo định lí Vi-ét , ta có : \(\hept{\begin{cases}x_1+x_2=\frac{-2\left(m-1\right)}{7}\\x_1.x_2=\frac{-m^2}{7}\end{cases}}\)
Khi đó : \(x_1^2+x_2^2=\left(x_1+x_2\right)^2-2.x_1.x_2\)
\(=\left[\frac{-2\left(m-1\right)}{7}\right]^2-2.\frac{-m^2}{7}\)
\(=\frac{4\left(m-1\right)^2}{49}+\frac{2m^2}{7}\)
\(=\frac{4m^2-8m+4+14m^2}{49}\)
\(=\frac{18m^2-8m+4}{49}\)

Phương trình bậc hai 3x2 + 5x + 2 = 0
Có a = 3; b = 5; c = 2; Δ = b2 – 4ac = 52 – 4.3.2 = 1 > 0
Áp dụng công thức nghiệm, phương trình có hai nghiệm phân biệt là:
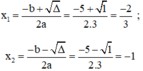
Vậy phương trình có hai nghiệm là -1 và 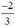
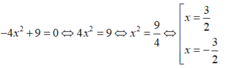
a^n-b^n= (a-b).(.......) với mọi n
Dùng công thức Niu tơn để tìm nghiệm của pt thì (a-b) chính là nghiệm đó bạn