VT
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
CM
7 tháng 5 2018
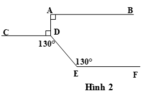
Ta có: A B ⊥ A D ; C D ⊥ A D (gt).
Þ AB // CD (vì cùng vuông góc với AD) (1)
Ta lại có: C D E ^ = E ^ = 130 o (gt)
Þ EF // CD (vì có cặp góc so le trong bằng nhau). (2)
Từ (1) và (2) Þ AB // EF (vì cùng song song với CD).
28 tháng 7 2023
a: XétΔABK vuông tại K và ΔADK vuông tại K có
AB=AD
AK chung
=>ΔABK=ΔADK
b: Xét ΔAEK vuông tại E và ΔAFK vuông tại F có
AK chung
góc EAK=góc FAK
=>ΔAEK=ΔAFK
=>AE=AF và KE=KF
=>ΔAEF cân tại A và ΔKEF cân tại K
c: AE=AF
KE=KF
=>AK là trung trực của EF
=>AK vuông góc EF
9 tháng 3 2022
F ở đâu bạn ?
b, Xét tam giác ABD và tam giác ACE
^A _ chung
AB = AC
Vậy tam giác ABD = tam giác ACE (ch-gn)
c, Ta có BD ; CE lần lượt là đường cao
mà BD giao CE = O
=> O là trực tâm tam giác ABC
=> AO là đường cao thứ 3 trong tam giác
mà tam giác ABC cân tại A nên AO là đường cao
đồng thời là đường phân giác ^BAC
Cho hình thang vuông ABCD có góc A = góc D = 90 độ, AB = AD = CD/2. Qua điểm E thuộc cạnh AB,kẻ đường vuông góc với DE cắt BC tại F. Chứng minh: ED = EF.
?
ko hiểu