Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Ta có: Nhiệt lượng Q = m c ∆ t
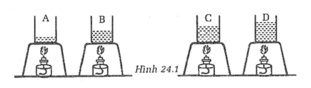
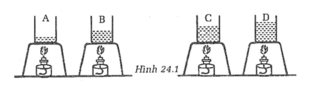
Bình A chứa lượng nước ít nhất (1l) trong các bình
=> trong cùng một thời gian đun trên bếp cồn như nhau thì nhiệt độ trong bình A là cao nhất

Bình A chứa lượng nước ít nhất trong các bình ⇒ Trong cùng một thời gian đun trên bếp cồn như nhau thì nhiệt độ trong bình A là cao nhất
⇒ Đáp án A

A
Bình A chứa lượng nước ít nhất (1l) trong các bình.
=> Trong cùng một thời gian đun trên bếp cồn như nhau thì nhiệt độ trong bình A là cao nhất.
=> Chọn A.

Chọn A vì các vật đều được đun bằng những đèn cồn giống nhau, nước ban đầu ở cùng một nhiệt độ. Do lượng nước trong bình A ít nhất nên nhiệt độ ở bình A là cao nhất.

Chọn C vì độ tăng nhiệt độ và chất cấu tạo nên vật đều giống nhau nên nhiệt độ của các bình khác nhau do lượng chất lỏng chứa trong từng bình đó .

B
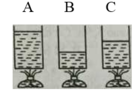
Thể tích chất lỏng càng ít thì nhiệt độ tăng càng cao, vậy nhiệt độ của chất lỏng ờ bình B cao nhất, rồi đến bình C, bình A.

m1 = 4kg
m2 = 1kg
a) Gọi m là khối lượng nước rót từ bình 1 sang bình 2 và ngược lại.
+ Quá trình rót nước từ 1 sang 2, nhiệt độ cân bằng bình 2 là t1: \(Q_{tỏa}=Q_{thu}\)
\(\Rightarrow m.c(50-t_1)=1.c(t_1-30)\) (1)
+ Quá trình rót nước từ 2 trở về 1, nhiệt độ cân bằng là \(48^0C\), phương trình cân bằng nhiệt:
\(m.c(48-t_1)=(4-m).c.(50-48)\Rightarrow m.c(50-t_1)=8c\) (2)
Từ (1) và (2) suy ra: \(c(t_1-30)=8c\Rightarrow t_1=38^0C\)
b) Từ (1) ta có: \(m.c(50-38)=c(38-30)\Rightarrow m=\dfrac{2}{3}(kg)\)

- Gọi lượng nước rót mỗi lần là x ( lít); nhiệt độ cân bằng nhiệt ở bình B là t0(0C); nhiệt dung riêng của nước là c( J/kg.độ); với nước thì 1lít= 1kg
- Lần rót 1: Từ bình A sang bình B ta có phương trình cân bằng nhiệt ở bình B:
x.c.(60 – t0) = 1.c.(t0 – 20)
↔ x.(60 – t0) = (t0 – 20)
↔ x = \(\frac{t_0-20}{60-t_0}\) (1)
- Lần rót 2: Từ bình B sang bình A ta có phương trình cân bằng nhiệt ở bình A:
(5-x).c(60-59) = x.c.(59- t0)
↔ 5-x = x.(59- t0) (2)
- Từ (1;2) ta có: 5- \(\frac{1_0-20}{60-t_0}\)= \(\frac{t_0-20}{60-t_0}\).(59- t0)
↔5.(60-t0)- t0 + 20 = (t0- 20).(59-t0)
↔300- 5t0 –t0 +20 = 59.t0- t02 – 1180 +20.t0
↔t02 – 85.t0 + 1500 = 0.
Giải ra được t0 = 25 (0C) thay vào (1) được x = 1/7( lít)

ta có:
khi rót từ bình một sang hai thì phương trình cân bằng nhiệt là:
\(Q_{tỏa}=Q_{thu}\)
\(\Leftrightarrow mC\left(t_1-t\right)=m_2C\left(t-t_2\right)\)
\(\Leftrightarrow m\left(90-t\right)=t-10\)
\(\Rightarrow m=\frac{t-10}{90-t}\left(1\right)\)
khi rót lại rừ hai sang một thì phương trình cân bằng nhiệt là:
\(Q_{tỏa}=Q_{thu}\)
\(\Leftrightarrow\left(m_1-m\right)C\left(t_1-t'\right)=mC\left(t'-t\right)\)
\(\Leftrightarrow12\left(4-m\right)=m\left(78-t\right)\)
\(\Leftrightarrow48-12m=78m-mt\)
\(\Leftrightarrow mt=78m-48+12m\)
\(\Leftrightarrow90m-mt=48\)
\(\Rightarrow m=\frac{48}{90-t}\)
\(\Leftrightarrow\frac{t-10}{90-t}=\frac{48}{90-t}\)
\(\Leftrightarrow t-10=48\Rightarrow t=58\) độ C
\(\Rightarrow m=1,5kg\)
Đáp án D
Ta có: Nhiệt lượng : Q = mc ∆ t
Bình D chứa lượng nước nhiều nhất (4l) trong các bình
=> trong cùng một thời gian đun trên bếp cồn như nhau thì nhiệt độ trong bình D là thấp nhất