Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Câu hỏi của Phạm Thị Hường - Toán lớp 8 - Học toán với OnlineMath
Em tham khảo bài làm ở link này nhé!

Nhận xét :
\(\dfrac{1}{k^3}< \dfrac{1}{2}\left(\dfrac{1}{\left(k-1\right)k}-\dfrac{1}{k\left(k+1\right)}\right)\)
Áp dụng nhận xét trên ta có:
\(=>B< \dfrac{1}{2}\left(\dfrac{1}{2.3}-\dfrac{1}{3.4}+\dfrac{1}{3.4}-\dfrac{1}{4.5}....+\dfrac{1}{\left(n-1\right)n}-\dfrac{1}{n\left(n+1\right)}\right)\)
\(=>B< \dfrac{1}{2}\left(\dfrac{1}{2.3}-\dfrac{1}{n\left(n+1\right)}\right)< \dfrac{1}{12}\)
\(=>B< \dfrac{1}{12}\)
CHÚC BẠN HỌC TỐT..................
\(\)

Bổ đề : \(x^3+y^3\ge xy\left(x+y\right)=x^2y+xy^2\)
C/m bổ đề : \(x^3+y^3\ge xy\left(x+y\right)\)
\(\Leftrightarrow x^2-2xy+y^2\ge0\)
\(\Leftrightarrow\left(x-y\right)^2\ge0\)
Vậy bổ đề đúng .
Áp dụng vào bài toán
\(\dfrac{1}{x^3+y^3+1}+\dfrac{1}{y^3+z^3+1}+\dfrac{1}{z^3+x^3+1}\le1\)
Ta có : \(x^3+y^3+1\ge xy\left(x+y\right)+1=xy\left(x+y\right)+xyz=xy\left(x+y+z\right)\)
\(\Leftrightarrow\dfrac{1}{x^3+y^3+1}\le\dfrac{xyz}{xy\left(x+y+z\right)}=\dfrac{z}{x+y+z}\)
Chứng minh tương tự ta được : \(\dfrac{1}{y^3+z^3+1}\le\dfrac{x}{x+y+z}\)
\(\dfrac{1}{z^3+x^3+1}\le\dfrac{y}{x+y+z}\)
Cộng từng về ta được :
\(\dfrac{1}{x^3+y^3+1}+\dfrac{1}{y^3+z^3+1}+\dfrac{1}{z^3+x^3+1}\ge\dfrac{x+y+z}{x+y+z}=1\)
=> ĐPCM .
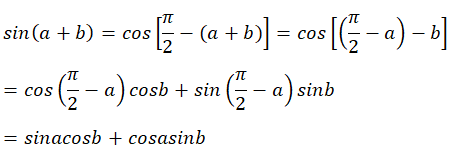


Không mất tính tổng quát giả sử: \(A\ge B\ge C\)
=> \(tanA\ge tanB\ge tanC;cosA\le cosB\le cosC\)
Áp dụng BĐT Chebyshev ta có:
\(\left(\dfrac{tanA+tanB+tanC}{3}\right)\left(\dfrac{cosA+cosB+cosC}{3}\right)\ge\dfrac{tanA\cdot cosA+tanB\cdot cosB+tanC\cdot cosC}{3}\)
=> \(\dfrac{sinA+sinB+sinC}{cosA+cosB+cosC}\le\dfrac{tanA+tanB+tanC}{3}\)
mặt khác ta có: \(tanA+tanB+tanC=tanA\cdot tanB\cdot tanC\)
=> \(\dfrac{sinA+sinB+sinC}{cosA+cosB+cosC}\le\dfrac{tanA\cdot tanB\cdot tanC}{3}\left(đpcm\right)\)
đẳng thức xảy ra khi tam giác ABC đều
Đề sai.
\(tan90^o=\dfrac{1}{0}\) (không thể chia cho không) nên đề bài sai với trường hợp tam giác vuông rồi.