Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Gọi H, K lần lượt là trung điểm của BC, C'A'
\(\Delta A'BC'\)cân tại B có \(\widehat{A'BC'}=120^0\)\(\Rightarrow\widehat{BC'A'}=\widehat{BA'C'}=30^0\)
\(\Rightarrow\Delta BKC'\)là nửa tam giác đều
\(\Rightarrow BK=\frac{1}{2}BC'\)(1)
\(AH\perp BC\)(do \(\Delta ABC\)đều) nên \(\Delta ABH\)là nửa tam giác đều
\(\Rightarrow BH=\frac{1}{2}AB\)(2)
Từ (1) và (2) suy ra \(\frac{BK}{BC'}=\frac{BH}{AB}\)
Ta có: \(\widehat{KBH}=60^0-\widehat{ABK}=\widehat{ABC'}\)
\(\Delta KBH\)và \(\Delta C'BA\)có: \(\frac{BK}{BC'}=\frac{BH}{BA}\left(cmt\right)\); \(\widehat{KBH}=\widehat{C'BA}\left(cmt\right)\)
\(\Rightarrow\Delta KBH~\Delta C'BA\left(c-g-c\right)\)
\(\Rightarrow\frac{KH}{C'A}=\frac{1}{2}\Rightarrow\frac{KH}{AB'}=\frac{1}{2}\)và \(\widehat{C'AB}=\widehat{KHB}\)
Ta có: \(\widehat{HAB'}=\widehat{B'AC'}-\left(30^0+\widehat{C'AB}\right)\)
\(=\left(\widehat{B'AC'}-30^0\right)-\widehat{C'AB}=90^0-\widehat{KHB}=\widehat{KHA}\)
Mà \(\widehat{HAB'}\)và \(\widehat{KHA}\)ở vị trí so le trong nên KH // AB'
\(\Rightarrow\frac{KG}{GB'}=\frac{GH}{GA}=\frac{KH}{AB'}=\frac{1}{2}\)
hay \(\frac{B'G}{KB'}=\frac{GA}{HA}=\frac{2}{3}\)
Điều này chứng tỏ \(\Delta ABC\)và \(\Delta A'B'C'\)có cùng trọng tâm (đpcm)

hình tự vẽ nha. lười quá
Kẻ trung tuyến CM,DN của \(\Delta ACD\)( M,N \(\in\)AB,AC )
AM và DN cắt nhau ở E. gọi Giao điểm của CD và AO là I
dễ dàng suy ra I là trọng tâm của \(\Delta ABC\)
Ta có : \(\frac{CE}{CM}=\frac{CI}{CD}=\frac{2}{3}\Rightarrow EI//AB\)
Mà \(OD\perp AB\)nên \(EI\perp OD\)( 1 )
Lại có : \(OI\perp BC\)mà BC // DN nên \(OI\perp DN\)( 2 )
Từ ( 1 ) và ( 2 ) suy ra I là trực tâm của \(\Delta ODE\), do đó OE \(\perp\)DI
Hay \(OE\perp CD\)

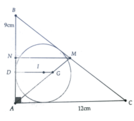
Gọi M là trung điểm của BC
Ta tính được AG = 2 3 AM = 10cm
Gọi N là trung điểm của AB => MN//AC, MN ⊥ AB
D,I,G thẳng hàng
<=> A G A M = A D A N = 2 3 <=> A D 2 A N = 1 3 <=> A D A B = 1 3
Ta có AD = r nội tiếp = A B + A C - B C 2 <=> A B 3 = A B + A C - B C 2
<=> AB+3AC = 3BC = A B 2 + A C 2
<=> 3AC = 4AB (đpcm)
Áp dụng kết quả trên ta có: AD = A B + A C - B C 2 = 3cm
=> ID = DA = 3cm => IG = DG – ID = 1cm

a: Xét (O) có
ΔABD nội tiếp
AD là đường kính
Do đó: ΔABD vuông tại B
=>BD//CH
Xét (O) có
ΔACD nội tiếp
AD là đường kính
Do đó: ΔACD vuông tại C
=>CD//BH
Xét tứ giác BHCD có
BH//CD
BD//CH
Do đó: BHCD là hình bình hành
b: BHCD là hình bình hành
nên BC cắt HD tại trung điểm của mỗi đường
=>I là trung điểm của HD
Xét ΔDAH có DI/DH=DO/DA
nen Io//AH và IO=AH/2
=>AH=2OI
c: G là trọng tâm
nên AG=2AI
Xét ΔAHD có
AI là trung tuyến
AG=2/3AI
DO đó: G là trọng tâm

khó dữ dzậy
đậu xanh hình 9