Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

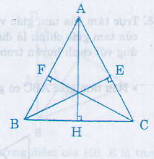
Xét hai tam giác vuông EBC và FCB có:
BC (cạnh huyền chung)
BE = CF
Vậy ∆EBC = ∆FCB (cạnh huyền cạnh góc vuông)
=>
hay ∆ABC cân tại A
+ Nếu tam giác có ba đường cao bằng nhau, tương tự như chứng minh trên, ta chứng minh được đó là tam giác đều.

Gọi I là giao điểm của hai đường phân giác xuất phát từ đỉnh B và đỉnh C của tam giác ABC.
- Vì I nằm trên tia phân giác BE của góc B nên IL = IH (1) (theo định lí 1 về tính chất của tia phân giác).
- Tương tự, ta có IK = IH (2).
- Từ (1) và (2) suy ra IK = IL (= IH), hay I cách đều hai cạnh AB, AC của góc A. Do đó I nằm trên tia phân giác của góc A (theo định lí 2 về tính chất của tia phân giác), hay AI là đường phân giác xuất phát từ đỉnh A của tam giác ABC.
Tóm lại, ba đường phân giác của tam giác ABC cùng đi qua điểm I và điểm này cách đều ba cạnh của tam giác, nghĩa là : IH = IK = IL.

Xét tam giác ABC cân tại A, đường phân giác AH.
Xét tam giác BAH và tam giác CAH có:
AB=AC (do tam giác ABC cân tại A)
\(\widehat{BAH}=\widehat{CAH}=\frac{\widehat{A}}{2}\)
AH chung
=> \(\Delta BAH=\Delta CAH\left(c.g.c\right)\)
=> \(\widehat{AHB}=\widehat{AHC}\)
Mà \(\widehat{AHB}+\widehat{AHC}=180^o\)(kề bù)
=>\(\widehat{AHB}=\widehat{AHC}=\frac{180^o}{2}=90^o\)
=>AH L BC
Ngược lại c/m tương tự

A B C E D
-Tam giác ABC cân tại A có BE và CD là 2 đtt
=> AB=AC => AE=AD
Xét tgABE , tgACD có góc A chung , AE=AD,AB=AC
=> ABE=ACD (c g c)
=>BE=CD
-Tam giác ABC có BE và CD là 2 đtt bằng nhau và cắt tại G
=> EG=DG , BG=CG
\(\Delta DGB\),\(\Delta EGC\) có gocDGB = gocEGC ( 2 góc đối đình) EG=DG, BG=CG
=>\(\Delta DGB\)=\(\Delta EGC\)(c.g.c)
=>BD=EC
Xét \(\Delta EBC\) và \(\Delta DCB\) có: BE=CD , BC chung, BD=EC
=>\(\Delta EBC\)=\(\Delta DCB\) (c.c.c)
=>\(\widehat{EBC}=\widehat{DCB}\)
=> TgABC cân tại A (đpcm)
kho lam tao chiu