Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(P=\dfrac{\left(cos^2x-sin^2x\right)^2}{4sin^2x.cos^2x}-\dfrac{1}{4sin^2x.cos^2x}=\dfrac{\left(cos^2x-1-sin^2x\right)\left(cos^2x+1-sin^2x\right)}{4sin^2x.cos^2x}\)
\(=\dfrac{-2sin^2x.2cos^2x}{4sin^2x.cos^2x}=-1\)
\(y^2-3y-1=0\) có \(ac=-1< 0\Leftrightarrow\) có 2 nghiệm trái dấu hay có 1 nghiệm dương

Đề bài không chính xác, biểu thức này vẫn phụ thuộc a
Đề bài đúng phải là: \(\sqrt{sin^4a+4cos^2a}+\sqrt{cos^4a+4sin^2a}\)

TL:
Bạn tham khảo cái link này nha https://vietjack.com/giai-toan-10-nang-cao/bai-49-trang-215-sgk-dai-so-10-nang-cao.jsp
~ t.i.c.k cho mk nha , học tốt ~

Đề bài không sai, biểu thức vẫn phụ thuộc A
Phản ví dụ: với \(a=0\Rightarrow A=2\)
Với \(a=\dfrac{\pi}{2}\Rightarrow A=-13\)
Rõ ràng \(2\ne-13\)
Biểu thức đúng:
\(A=2\left(sin^6a+cos^6a\right)-3\left(sin^4a+cos^4a\right)\)

\(sin^8x-cos^8x-4sin^6x+6sin^4x-4sin^2x\)
\(=sin^8x-\left(1-sin^2x\right)^4-4sin^6x+6sin^4x-4sin^2x\)
\(=sin^8x-\left(1-4sin^2x+6sin^4x-4sin^6x+sin^8x\right)-4sin^6x+6sin^4x-4sin^2x\)\(=-1\) (bạn chép nhầm đề)
b/ \(\frac{sin6x+sin2x+sin4x}{1+cos2x+cos4x}=\frac{2sin4x.cos2x+sin4x}{1+cos2x+2cos^22x-1}=\frac{sin4x\left(2cos2x+1\right)}{cos2x\left(2cos2x+1\right)}=\frac{sin4x}{cos2x}=\frac{2sin2x.cos2x}{cos2x}=2sin2x\)
c/ \(\frac{1+sin2x}{cosx+sinx}-\frac{1-tan^2\frac{x}{2}}{1+tan^2\frac{x}{2}}=\frac{sin^2x+cos^2x+2sinx.cosx}{cosx+sinx}-\left(1-tan^2\frac{x}{2}\right)cos^2\frac{x}{2}\)
\(=\frac{\left(sinx+cosx\right)^2}{sinx+cosx}-\left(cos^2\frac{x}{2}-sin^2\frac{x}{2}\right)=sinx+cosx-cosx=sinx\)
d/ \(cos4x+4cos2x+3=2cos^22x-1+4cos2x+3\)
\(=2\left(cos^22x+2cos2x+1\right)=2\left(cos2x+1\right)^2=2\left(2cos^2x-1+1\right)^2=8cos^4x\)
e/

Lời giải:
Đề bài phải thêm đk về x. VD: \(x\in (-\frac{\pi}{2};0)\)
Ta có:
\(\sqrt{4\sin ^4x+\sin ^2(2x)}=\sqrt{4\sin ^4x+(2\sin x\cos x)^2}\)
\(=\sqrt{4\sin ^2x(\sin ^2x+\cos ^2x)}=\sqrt{4\sin ^2x}=|2\sin x|=-2\sin x\) do \(x\in (\frac{-\pi}{2};0)\)
Mặt khác:
\(\cos \left(\frac{\pi}{4}-\frac{x}{2}\right)=\cos \frac{\pi}{4}\cos \frac{x}{2}+\sin \frac{\pi}{4}\sin \frac{x}{2}\)
\(=\frac{\sqrt{2}}{2}\cos \frac{x}{2}+\frac{\sqrt{2}}{2}\sin \frac{x}{2}\)
\(\Rightarrow 4\cos ^2\left(\frac{\pi}{4}-\frac{x}{2}\right)=2(\cos \frac{x}{2}+\sin \frac{x}{2})^2\)
\(=2(\cos ^2\frac{x}{2}+\sin ^2\frac{x}{2}+2\cos \frac{x}{2}\sin \frac{x}{2})\)
\(=2(1+\sin x)=2+2\sin x\)
Do đó: \(A=-2\sin x+2+2\sin x=2\) không phụ thuộc vào x

Lời giải:
Ta có:
\(\sin ^2x\tan ^2x+4\sin ^2x-\tan ^2x+3\cos ^2x\)
\(=\tan ^2x(\sin ^2x-1)+4\sin ^2x+3\cos ^2x\)
\(=\tan ^2x(-\cos ^2x)+4\sin ^2x+3\cos ^2x\)
\(=\left(\frac{\sin x}{\cos x}\right)^2(-\cos ^2x)+4\sin ^2x+3\cos ^2x\)
\(=-\sin ^2x+4\sin ^2x+3\cos ^2x\)
\(=3(\sin ^2x+\cos ^2x)=3\)
Vậy giá trị của biểu thức không phụ thuộc vào $x$
Ta có đpcm.
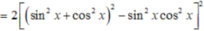

 không phụ thuộc vào x.
không phụ thuộc vào x.