Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1) Hai đồ thị gọi là đối xứng với nhau qua trục hoành nếu f(x)+f(x)'=0
Do:
f(x)=x-2,f(x)'=2-x và f(x)+f(x)'=0=>Chúng đối xứng với nhau qua trục hoành.

Đáp án :
B. Đồ thị hàm số chẵn nhận trục hoành làm trục đối xứng.

1: Theo đề, ta có:
-b/2*(-1)=5/2
=>-b/-2=5/2
=>b=5
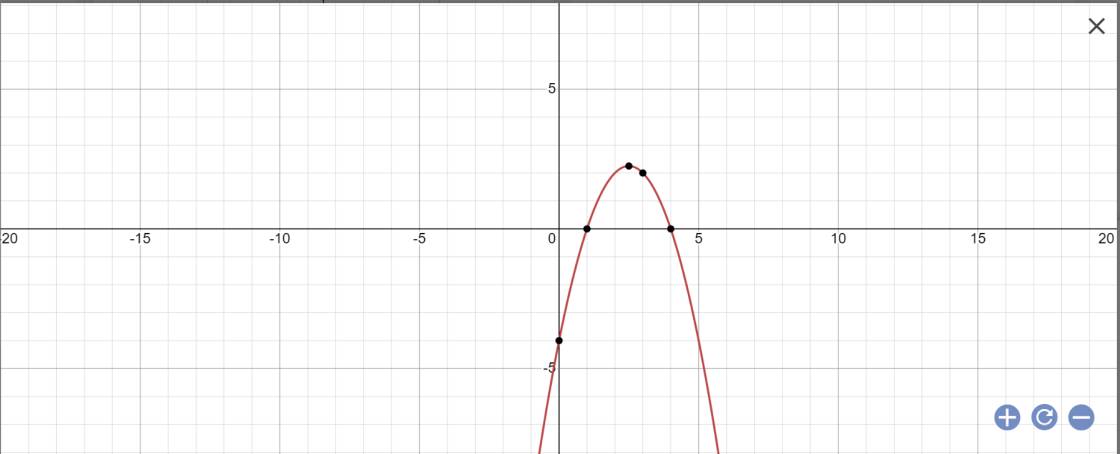
2: y=-x^2+5x-4

Gọi công thức của hàm số bậc hai là \(y=ax^2+bx+c\)
Trục đối xứng là x=3 nên \(-\dfrac{b}{2a}=3\)
=>b=-2a
Thay x=0 và y=-16 vào (d), ta được:
\(a\cdot0^2+b\cdot0+c=-16\)
=>c=-16
=>\(y=ax^2+bx-16\)
Thay x=-2 và y=0 vào (d), ta được:
\(a\cdot\left(-2\right)^2+b\left(-2\right)-16=0\)
=>4a-2b-16=0
=>\(4a-2\cdot\left(-2a\right)=16\)
=>8a=16
=>a=2
=>b=-2a=-4
Vậy: Công thức cần tìm là \(y=2x^2-4x-16\)

a: Thay x=3 và y=0 vào (1), ta được:
\(6-3m=0\)
hay m=2

a: \(\left\{{}\begin{matrix}x_I=\dfrac{3}{2\cdot1}=\dfrac{3}{2}\\y_I=-\dfrac{\left(-3\right)^2-4\cdot1\cdot\left(-2\right)}{4\cdot1}=-\dfrac{17}{4}\end{matrix}\right.\)
2 đồ thị \(y=f\left(x\right)\) và \(y=g\left(x\right)\) đối xứng nhau qua trục hoành khi \(g\left(a\right)=-f\left(a\right)\) \(\forall a\in TXĐ\)
Đặt \(y=f\left(x\right)=x-2\) ; \(y=g\left(x\right)=2-x\)
Với 1 số thực a bất kì, ta có:
\(y\left(a\right)=f\left(a\right)=a-2\)
\(y\left(a\right)=g\left(a\right)=2-a=-\left(a-2\right)=-f\left(a\right)\)
\(\Rightarrow y=x-2\) và \(y=2-x\) đối xứng qua trục hoành