1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
8 tháng 7 2017
a)\(P=\dfrac{2012}{x^2+4x+2013}\)
Ta thấy: \(x^2+4x+2013=x^2+4x+4+2009\)
\(=\left(x+2\right)^2+2009\ge2009\)
\(\Rightarrow\dfrac{1}{\left(x+2\right)^2+2009}\le\dfrac{1}{2009}\)
\(\Rightarrow P=\dfrac{2012}{\left(x+2\right)^2+2009}\le\dfrac{2012}{2009}\)
Xảy ra khi \(x=-2\)
LM
30 tháng 9 2016
N =\(\frac{2010+2011+2012}{2011+2012+2013}\)
\(\Rightarrow N=\frac{2010}{2011+2012+2013}+\frac{2011}{2011+2012+2013}+\frac{2012}{2011+2012+2013}\)
Do: \(\frac{2010}{2011}>\frac{2010}{2011+2012+2013};\frac{2011}{2012}>\frac{2011}{2011+2012+2013};\frac{2012}{2013}>\frac{2012}{2011+2012+2013}\)
\(\Rightarrow\frac{2010}{2011}+\frac{2011}{2012}+\frac{2012}{2013}>\frac{2010}{2011+2012+2013}+\frac{2011}{2011+2012+2013}+\frac{2012}{2011+2012+2013}\)
\(\Rightarrow\frac{2010}{2011}+\frac{2011}{2012}+\frac{2012}{2013}>\frac{2010+2011+2012}{2011+2012+2013}\Leftrightarrow N>M\)
NV
1
27 tháng 5 2020
Ko bt trình bày kiur chi ... lm nè :3 not thể hiện >:
Đặt đa thức trên là A
\(A=4x^2-x+6=0\)
Ta có : \(\left(-1\right)^2-4.6.4=1-96=-95< 0\)
Nên phương trình vô nghiệm
Suy ra : Đa thức ko có nghiệm.
21 tháng 3 2018
Ta có :
\(\frac{1}{2013}M=\frac{2013^{2012}+2012}{2013^{2012}+2013}=\frac{2013^{2012}+2013}{2013^{2012}+2013}-\frac{1}{2013^{2012}+2013}=1-\frac{1}{2013^{2012}+2013}\)
Lại có :
\(\frac{1}{2013}N=\frac{2013^{2011}+2012}{2013^{2011}+2013}=\frac{2013^{2011}+2013}{2013^{2011}+2013}-\frac{1}{2013^{2011}+2013}=1-\frac{1}{2013^{2011}+2013}\)
Vì \(\frac{1}{2013^{2012}+2013}< \frac{1}{2013^{2011}+2013}\) nên \(M=1-\frac{1}{2013^{2012}}>N=1-\frac{1}{2013^{2011}+2013}\)
Vậy \(M>N\)
Chúc bạn học tốt ~
VM
7 tháng 1 2020
\(f\left(x\right)=4x^2+3x+1\)
\(g\left(x\right)=3x^2-2x+1.\)
a) \(h\left(x\right)=f\left(x\right)-g\left(x\right)\)
\(\Rightarrow h\left(x\right)=\left(4x^2+3x+1\right)-\left(3x^2-2x+1\right)\)
\(\Rightarrow h\left(x\right)=4x^2+3x+1-3x^2+2x-1\)
\(\Rightarrow h\left(x\right)=\left(4x^2-3x^2\right)+\left(3x+2x\right)+\left(1-1\right)\)
\(\Rightarrow h\left(x\right)=x^2+5x.\)
b) Ta có \(h\left(x\right)=x^2+5x.\)
Đặt \(x^2+5x=0\)
\(\Rightarrow x.\left(x+5\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=0\\x+5=0\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=0\\x=0-5\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=0\\x=-5\end{matrix}\right.\)
Vậy \(x=0\) và \(x=-5\) là các nghiệm của đa thức \(h\left(x\right).\)
Chúc bạn học tốt!
DQ
0
DA
4 tháng 4 2017
\(x^2+4x+2013=x^2+4x+4+2009=\left(x+2\right)^2+2009\ge2009\)
\(\Rightarrow P\le\frac{2012}{2009}\)
\(\frac{a^{2012}+2011}{a^{2012}+2011}+\frac{3}{a^{2012}+2011}=1+\frac{3}{a^{2012}+2011}\\ Qmax\Leftrightarrow a^{2012}min\Leftrightarrow a=0\)
Thay vào là ra
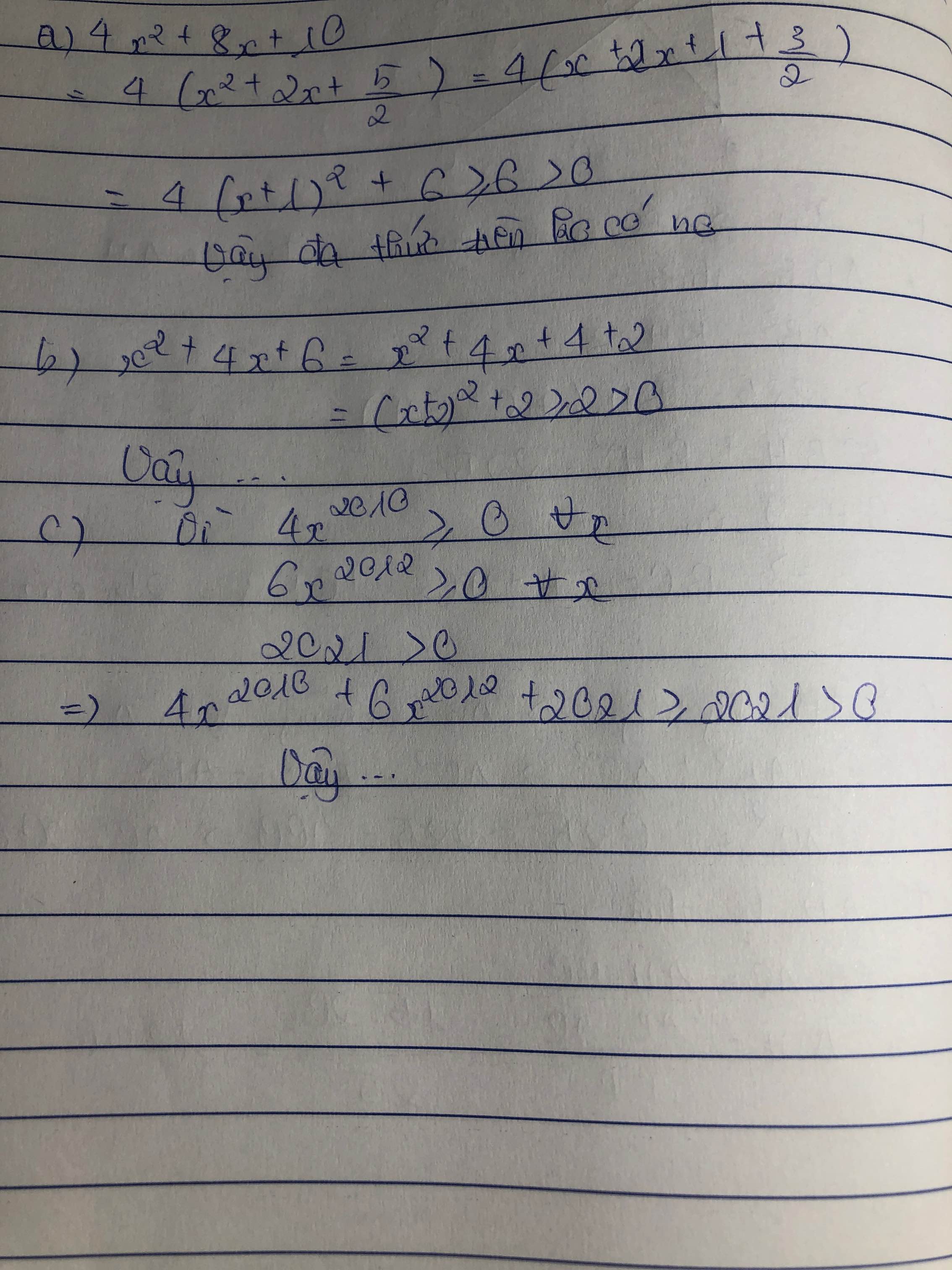
Ta có: \(4x^{2010}\ge0\)với mọi x và \(46x^{2012}\ge0\)với mọi x
Vậy: \(4x^{2010}+6x^{2012}+2013\ge2013\)với mọi x
\(\Rightarrow4x^{2010}+6x^{2012}+2013\ne0\)với mọi \(x\inℝ\)
Vậy đa thức \(\Rightarrow4x^{2010}+6x^{2012}+2013\)ko có nghiệm trong \(ℝ\)